Приступая к общей характеристике объектов восприятия, будем различать их объективные и субъективные характеристики, а также характеристики, зависящие от условий восприятия. Объективные характеристики в свою очередь могут быть разделены на структурные (синтаксические) и смысловые (семантические). Далее всюду, где это не оговорено, речь будет идти о структурных характеристиках.
Рассмотрим в качестве характеристик классификационные признаки, взятые по различным основаниям. Прежде всего, разделим целостные объекты восприятия по основным признакам целого — связности, ограниченности, полноте и компактности. Для иллюстрации такого деления воспользуемся геометрической интерпретацией на плоскости. По степени связности будем различать несвязные, квазисвязные, многосвязные и односвязные объекты (рис. 3, а—г), по характеристикам границы — неограниченные, частично ограниченные и ограниченные (рис. 3, д—ж), по полноте — неполные, полные и избыточно полные, по компактности — слабокомпактные (диффузные), компактные и сильнокомпактные (плотные) объекты.
Для объективного разделения несвязных и квазисвязных объектов можно ввести следующий критерий. Объект считается квазисвязным, если наименьшее расстояние между его связными областями меньше максимального линейного размера его областей. Например, для объекта на рис. 3, а это условие не выполняется (mn < pq), а для объекта на рис. 3, б оно выполнено (mn > pq). Введенный таким образом критерий хорошо выполняется для квазисвязных объектов восприятия, независимо от размеров объекта и модальности восприятия. Так, расстояния между частями архитектурного ансамбля не превосходят, как правило, максимальных линейных размеров его частей, паузы в музыкальном тексте короче времени звучания и т. д.
В некоторых «хороших» фигурах (например, в фигуре, состоящей из точек, расположенных в вершинах правильного многоугольника) элементы могут оказаться ни связными, ни квазисвязными в пространстве объекта. Связность элементов в этом случае осуществляется в пространстве признаков. В приведенном примере фигуры из точек таким признаком является признак положения элемента по отношению к остальным элементам.

Ограниченность в пространстве или времени является необходимым условием разделения объекта и среды (предмета и фона). Среда (фон) связна, но не ограничена, и в этом одно из отличий объекта и среды. Граница есть область разрыва (или область больших градиентов) одной из функций, определенных в пространстве объект — среда, другие же функции в той же области должны быть непрерывными. В результате этого объект, с одной стороны, выделяется из среды, а с другой, — сохраняет с нею органическую связь. Неограниченность — не единственное отличие фона от фигуры. Фон и фигура имеют разную топологию, метрику и размерность. На процесс восприятия оказывают большое влияние такие характеристики фона, как степень его стационарности и активности. Существенно также и то, что фон воспринимается субъектом раньше объекта и более длительное время.
Основными объективными характеристиками являются пространственные (положение, величина), временные (положение во времени, длительность). Весьма важной для восприятия характеристикой является число элементов или частей объекта. По временным характеристикам объекты можно разделить на статические и динамические, на стационарные и нестационарные. Отчетливо разделяются объекты восприятия по числу и составу измерений пространства и времени. Всего возможны 7 таких классов: T, LT — музыка; L2T — кино, телевизор; L3T — танец, спектакль, стереокино; L3 — скульптура, архитектура, реальные объекты; L2 — фотография, проекция на поверхность; L — не существует реальных объектов, имеющих только одно временное или пространственное измерение.
Целостный объект восприятия является носителем информации для субъекта. С этой точки зрения он может быть охарактеризован количественно (количеством информации) и качественно (с точки зрения синтактики, эстетики, семантики и прагматики). Интегральной характеристикой объектов восприятия является степень их гармоничности (в смысле реализации в них принципов гармоничности целого). Наконец, будем различать реальные целостные объекты, их отображения и концептуальные целостные объекты. Особенности восприятия объектов этих трех классов рассматриваются в главе V. Отметим также, что целостные объекты восприятия в своем большинстве относятся к статическим системам, которые в общей теории систем не рассматриваются.
В связи с проблемой распознавания были разработаны различные методы описания объектов восприятия. Описания, позволяющие восстановить объект с наперед заданной точностью, называются абсолютными, а не позволяющие сделать этого — относительными (терминология А. А. Харкевича). В зависимости от выбора алфавита все описания можно разделить на описания в пространстве рецепторов и описания в пространстве признаков. В первом случае объект проецируется па некоторую сетчатку (ретину) и изображение описывается набором состояний элементов ретины. В общем случае такое описание при помощи операции развертки приводится к n-мерному вектору. При этом сохраняются только топологические отношения близости элементов ретины в линии развертки. В этом случае и фигура и фон входят в описание изображения. Вариантом такого описания является координатное задание элементов фигуры. При большом числе элементов ретины такое описание получается весьма громоздким, и, кроме того, существенные отношения объекта содержатся в нем лишь в неявном виде.
При описании в пространстве признаков в качестве элементов берутся более крупные блоки объекта и выбирается словарь для описания как признаков элементов, так и отношений между ними. По виду применяемого математического аппарата все описания можно разделить на детерминированные и стохастические.
Имеются также попытки объединить «ретинное» и «признаковое» описание, проделать путь от точек до крупных блоков и изображения в целом. В этом случае описание объекта получается многоуровневым. Существует также группа методов, не требующая разложения объекта на элементы (спектральное описание изображений).
Специфика задачи опознания требует выделения информации, существенной для распознавания классов и устранения избыточной информации. Поэтому и описания оказывались относительными, выбирались такие свойства объектов, которые, во-первых, были специфичными отличительными признаками данного класса, а, во-вторых, были бы максимально инвариантными для заданной или возможно более широкой группы преобразований. Субъективные характеристики объектов восприятия: принадлежность к чувственной сфере субъекта, тип модальности (уни- или полимодальность), вид модальности, тип сигнала (первые и вторые сигналы), вид кода (символы или изображения), соотношение размеров рецептора и объекта и как следствие — симультанность или сукцессивность восприятия.
Условия восприятия во многом определяются соотношением свойства объекта и субъекта. Они во многом определяют возможность и необходимость действий субъекта. Объект может помещаться в перцептивном поле или превосходить его, объект восприятия может быть предметом и панорамой, различными могут быть и соотношения движения объекта и субъекта относительно среды (объект — план, объект — траектория движения наблюдателя как крайние случаи). Объекты зрительного и слухового восприятия, которые мы выбираем для дальнейшего рассмотрения, суть статические системы. А воспринимающий их человек — динамическая система. Процесс восприятия в этом случае есть процесс взаимодействия динамической системы человека и статической системы объекта.
В следующих четырех параграфах данной главы будут с единых позиций рассмотрены изображения, элементы музыки, текст, траектории движения.
Ограничим класс рассматриваемых объектов зрительного восприятия ограниченными, двумерными, ахроматическими полиградационными (или двуградационными) изображениями целостных объектов на нейтральном фоне без шумов. Внутри этого класса можно провести более детальную классификацию, например, выделить контурные и силуэтные изображения и т. д. В настоящее время предложены различные методы для описания объектов такого типа. Отметим, что эти методы носят преимущественно аналитический характер.
В качестве объектов для математического описания обычно берутся не любые объекты зрительного восприятия, а лишь некоторые их достаточно простые изображения. Это ограничение обусловлено желанием получить простые описания, пригодные для теоретического анализа или технической реализации. В рамках уже введенных ограничений обычно рассматривается более узкие классы: двуградационные и многоградационные изображения, а среди двуградационных — силуэтные и контурные.
Большая информативность контуров показана в многочисленных психологических экспериментах и хорошо объясняется информационной теорией. Контур может быть описан характеристической контурной функцией, полученной с помощью радиально-круговой или следящей развертки. Признаки контура в этих случаях суть некоторые функционалы от характеристической контурной функции. Эти способы описания могут быть названы аналитическими.
Другую группу способов составляют методы лингвистического или структурного анализа. Сущность этих методов состоит в следующем: система различных геометрических особенностей контурных изображений и множество правил их перечисления в описаниях образуют специальный язык на котором можно выразить сходства и отличия рассматриваемых изображений. Множество геометрических особенностей изображений образует словарь этого языка — словарь признаков. Множество правил построения описания из признаков образует порождающую грамматику этого языка. Структурный подход к описанию контуров дает возможность свести задачу описания сложного контура к совокупности задач локального анализа. Задача локального анализа контура заключается в том, чтобы обнаружить структурные элементы, измерить для них значение параметров и определить способ их соединения в структуру или их взаимное расположение. Основные типы операторов локального анализа можно условно разделить на следующие три категории: сглаживания, дифференцирования и выделения структурных элементов, оценки их формы и измерения параметров.
Кроме аналитических и структурных способов описания контурных изображений существуют еще статистические способы, используемые для оценки их сложности. Имеется целый ряд статистических характеристик, которые могут рассматриваться в качестве критерия сложности контура. К ним относятся, например, энтропия контура или средняя длина непрерывной последовательности точек, имеющих одинаковую яркость. Далее, такими характеристиками могут быть распределение узловых точек на контурных линиях, распределение расстояний между параллельными отрезками контуров и др. Для классификации контуров по их сложности могут быть использованы также моменты распределения яркости 1-го, 2-го и более высоких порядков.
Теперь рассмотрим способы математического описания ахроматических изображений, функция распределения яркости которых имеет более двух градаций. К ним относятся, прежде всего, запись изображения в виде прямоугольной числовой матрицы. Величина числа, являющегося элементом матрицы, пропорциональна значению функции яркости на данном изображения. Увеличение числа элементов этой матрицы позволяет сколь угодно точно воспроизвести любое изображение. Кроме того, можно дать описание ахроматического изображения при помощи составления радиально-круговых характеристических функций. Плоское ахроматическое изображение может быть представлено также в виде системы уравнений и неравенств, описывающих их составные части. Один из способов такого описания состоит в использовании обычных представлений о плоских геометрических объектах, взятых из аналитической геометрии и дополненной системой модифицированных операций алгебры логики (дизъюнкции, конъюнкции и отрицания), обладающих рядом специфических свойств. Уравнению удовлетворяют координаты точек, лежащих не контуре изображения, а его область описывается неравенством. Распределение яркости на изображении может быть представлено в виде функционала, заданного на области, ограниченной уравнением контура.
Изложенное выше дает некоторое представление о разнообразии существующих математических моделей плоских ахроматических объектов зрительного восприятия, пригодных в той или иной степени для технической реализации. Однако для рассмотрения возможности их использования в качестве моделей зрительного восприятия человека, а также для выяснения роли, которую играют отдельные части изображения (область и контур) в зрительном восприятии, необходимы дополнительные знания о структуре и особенностях этого процесса.
Модель изображения должна соответствовать задачам исследования, удовлетворять условиям целостности и современным представлениям о процессе и механизмах восприятия. В качестве модели рассмотрим класс двумерных ахроматических полиградационных изображений.
Декомпозиция, алфавиты и состав изображения. В опубликованных нами ранее работах [66] был сформулирован общий принцип квантования непрерывных стимулов и реакций. Сущность его состоит в следующем. Любой стимул и реакция многомерны, причем по одним измерениям их свойства во времени и пространстве непрерывны, по другим — имеют разрывы непрерывности или большие значения градиентов в отдельных точках. Здесь речь идет о таких свойствах объекта, которые фиксируются отображающей системой: интенсивность, кривизна линии, высота тона, размерность пространства и другие переменные. Точки разрывов непрерывности и являются точками естественного квантования стимулов и реакций. Этот принцип согласуется и с информационными представлениями. Свойства реального мира таковы, что вероятность непрерывности значительно выше вероятности разрывов или больших перепадов свойств. Разрывы маловероятны, и, вследствие этого, наиболее информативны.
Квантование сигнала всегда связано с искажениями. Поэтому весьма важно правильно выбрать число и расположение уровней квантования. Квантование с использованием свойств получателя сообщений позволяет значительно снизить величину искажений. В силу первичности топологических свойств именно они должны быть основой выделения элементов. Действительно, элемент по определению неразложим и, следовательно, обладает свойством связности (или квазисвязности). Но этим же свойством обладает и целое. Значит, это свойство целого повторяется во всех его элементах. Таким образом, элемент изображения есть связное, ограниченное или почти ограниченное множество точек плоскости ху, на котором функция яркости В(х, у) непрерывна. Все изображения есть совокупность таких элементов. Границами элементов является некоторое конечное число замкнутых или почти замкнутых линий разрыва непрерывности функции В(х, у). Каждая из таких линий (контуров) в свою очередь является связным множеством точек и может быть разложена на элементы, границами которых являются точки, в которых кривизна линии контура терпит разрыв. Следовательно, изображение разлагается на элементы трех типов: части плоскости, отрезки линии и точки (элементы 2-го, 1-го и 0-го порядка). Этот процесс разложения изображения на элементы можно представить в виде дерева. Как целое, так и злементы каждого уровня связаны. Таким образом, множество точек изображения может быть разложено на непересекающиеся подмножества — части плоскости (области), части границ областей (отрезки прямых и кривых) и точки (границы отрезков линий). Теперь появляется возможность говорить об алфавите изображения.
Алфавитом изображения являются точки, отрезки линий и ограниченные части плоскости, обладающие различными наборами признаков. Единственным признаком точки является ее положение в пространстве. Признаками отрезка линии помимо положения в пространстве являются ориентация, величина, кривизна. Признаки ограниченной части плоскости более многочисленны: положение, ориентация, величина, светлота и др. Если упорядочить признаки, характеризующие элементы всех типов, то каждому элементу можно поставить в соответствие вектор значений признаков, включая пустое значение для тех значений признаков, которыми данный элемент не обладает. Тогда объект может быть представлен в виде дерева, в узлах которого будут векторы элементов.
Элементы-области и элементы-границы качественно различны и образуют два различных алфавита. Элементы-области соответствуют сохранению, элементы-границы — изменению свойств объекта.
С помощью описанного способа можно произвести декомпозицию изображения на элементы, определить алфавит и статистические характеристики множества элементов. На основе такой декомпозиции определяется и состав изображения как целого. В отличие от элементов, части целого могут быть функциями элементов, могут пересекаться и должны иметь большее сходство с целым (§ 1, гл. II). Учет семантики накладывает дополнительные ограничения на определение частей целого.
Множества элементов и частей целого не совпадают. Так, для фигуры, изображенной на рис. 3, ж, элементами являются три внутренние области прямоугольников (1, 2 и 3), стороны этих прямоугольников (прямоугольные отрезки) и вершины углов прямоугольника. Составом этой фигуры являются прямоугольники 1, 2, 3, (1 + 2), (2 + 3), (1 + 2 + 3).
Этот же принцип декомпозиции (разбиения объекта восприятия на элементы) может быть применен в несколько измененном варианте. Известно, что любая физическая система, в том числе и отражающая система человека, обладает следующими принципиальными ограничениями: разрешающей способностью, чувствительностью, и полосой пропускания, что соответствует у человека пространственным, интенсивностным и временным дифференциальным порогам. Так, ограничение, накладываемое разрешающей способностью, приводит к тому, что две точки, близко расположенные друг к другу, воспринимаются как одна. Эти пороги определяют минимальные пространственно-временные и энергетические «размеры» элемента объекта восприятия, например, элементов телевизионного изображения. В этом случае речь идет также о реакции на изменение, на перепад, на разрыв непрерывности на уровне нижних порогов. Если ранее рассмотренный способ квантования объекта может быть соотнесен с перцептивным уровнем восприятия, то здесь можно говорить о сенсорном квантовании. Отличие его от перцептивного квантования только в параметре, претерпевающем изменение.
Структура изображения. Выше были рассмотрены вопросы декомпозиции, разложения изображения на части и элементы, адекватные восприятию человека. Но процессы анализа и синтеза непрерывно связаны между собой. Перейдем теперь к исследованию тех свойств объектов зрительного восприятия, которые обеспечивают объединение элементов в единое целое и являются объективной основой формирования целостного образа или впечатления. Ранее уже отмечалось (§ 1, гл. II), что при объединении элементов в систему в последней появляются свойства, которыми не обладали отдельные элементы. В значительной степени эти свойства обусловлены отношениями между элементами, частями и целым. При восприятии системы элементов воспринимаются не только сами элементы, их признаки и интегральные характеристики множества элементов и частей, но и отношения между элементами, их признаками и интегральными характеристиками. Поэтому отношения, наряду с такими факторами, как связность и ограниченность, играют решающую роль в объединении элементов в целостную, единую систему. Это обстоятельство делает необходимым детальное исследование отношений в объектах зрительного восприятия. Можно выделить следующие задачи объективного анализа отношений в объекте восприятия: 1) изучение свойств отношений отдельных классов; 2) исследование свойств особых отношений; 3) исследование свойств множества отношений в целом объекте; 4) введение интегральных оценок множества отношений; 5) исследование взаимосвязи интегральных оценок множества элементов и множества отношений; 6) построение алгебры отношений (для соответствующей модальности).
Множество, на котором определены отношения объекта восприятия, состоит из его элементов и самого объекта. Все отношения можно разделить на качественные и количественные. Первые в свою очередь делятся на отношения эквивалентности, сходства (толерантности) и порядка, вторые — на метрические и групповые.
Среди метрических отношений следует отметить ряд особых отношений. Наиболее важным является золотое отношение, являющееся иррациональным числом 0,618... Это отношение единственно в том смысле, что оно обладает одновременно и аддитивными и мультипликативными свойствами. Отношения, меньшие 0,618, мультипликативны с недостатком, а большие — с избытком.
Особыми являются также отношения первых чисел натурального ряда: ½, ⅔ и ¾. Так, в музыке отношение тем более консонантно, чем проще отношение: октава — ½, квинта — ⅔, кварта — ¾. В архитектуре весьма употребительны отношения √2 = 1,41, √3 = 1,73.
Классы отношений как вид связи играют неодинаковую роль. Одним из основных факторов при этом является число элементов: при малом числе элементов большую роль играют количественные отношения, при большом — качественные.
Какие отношения из числа тех, которые могут быть определены на множестве элементов изображения, определяют структуру последнего? Это группа отношений порядка по признакам пространственного положения (пространственная структура) и значимости (функциональная структура). Структура определяется способом декомпозиции и типом отношений. В ряде случаев декомпозиция изображения может быть выполнена не единственным образом. Для разных декомпозиций при одном и том же типе отношений может быть определено соответствующее число различных структур, каждая из которых может восприниматься. Возникает задача синтеза более сложной структуры (полиструктуры) из этих частных структур.
Интегральные характеристики изображений. Одним из результатов деятельности воспринимающих систем организма является глобальная оценка свойств изображений. Будем называть такие свойства интегральными. Среди них выделим интегралы по составу и интегралы по структуре. Интегралы по составу делятся на интегралы областей, интегралы границ и интегралы соотношения областей и границ. В результате такой интеграции получим признаки изображения как целого. Признаки могут быть получены двумя принципиально разными путями: интеграцией после декомпозиции и интеграцией без предварительной декомпозиции путем ряда параллельных преобразований. Рассмотрим вначале второй путь.
Введем понятие об эффективной площади целостного изображения. Любое изображение может быть вписано в круг, эллипс или прямоугольник некоторой минимальной величины. Выбор одной из этих фигур зависит от очертаний изображения. Величину площади этой фигуры (эллипса или прямоугольника) и будем называть эффективной площадью изображения Q.
Двуградационное изображение полностью описывается заданием яркости B в каждой точке его поверхности ху. Будем считать, что яркость может принимать одно из двух значений: 0 или 1 (белое или черное). Учитывая ограничения физических систем, можно допустить, что граница между черными и белыми областями изображения является гладкой линией, не имеет точек излома. Введем две количественные характеристики таких изображений. Первая из них — σ есть отношение площади, занимаемой черной областью Sч, к эффективной площади изображения Q:
σ = Sч / Q.
Для получения второй характеристики путем суммирования (или интегрирования) определим длину границы между черными и белыми областями изображения. Это будет суммарная длина линий всех контуров черно-белого изображения Р. Тогда отношение
λ = P / Q,
будет иметь смысл средней длины линии контура изображения, приходящейся на единицу эффективной площади изображения. Величина σ изменяется в пределах 0 ≤ σ ≤ 1, а λ — в пределах 0 ≤ λ ≤ λmax, λmax зависит от ширины переходной зоны между черными и белыми областями.
Величины σ и λ, не являются независимыми. Приведем пример такой зависимости для частного случая. Пусть изображение имеет форму квадрата и образовано из маленьких квадратных элементов (рис. 4). Площадь всего изображения (большого квадрата) примем за единицу. Тогда величина σ будет изменяться от нуля до единицы. Ее значения отложены по оси абсцисс (рис. 4, а). Задавшись величиной элемента изображения (в данном примере — малого квадратика), можно определить максимальное назначение
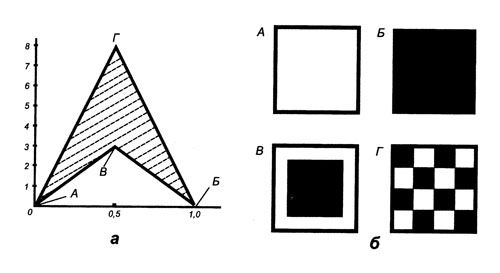
величины λ для изображений такого типа. Величина λ будет изменяться от нуля до λmax. На том же рисунке значения величины λ (в условных единицах) отложены по оси ординат. Своего наибольшего значения величина λ достигает при σ = 0,5. Изображение в этом случае имеет вид шахматной доски.
Заштрихованная область на рис. 4, а, есть область допустимых значений для пары чисел σ, λ. На рис. 4, б приведены изображения, соответствующие точкам А, Б, В и Г из упомянутой области допустимых значений. (Часть контура изображения, совпадавшая с границами всего изображения, при определении λ не учитывалась.)

Интегральные характеристики σ и λ могут быть определены без предварительного разложения на элементы. Назовем их характеристиками первого рода. Определим величины σ и λ для изображений двух классов: 1) букв русского алфавита, выполненных прямоугольным брусковым шрифтом; 2) товарных знаков [67]. Образцы объектов первого класса приведены на рис. 5 , второго — на рис. 6. В выборках было: 31 буква алфавита и 25 товарных знаков.
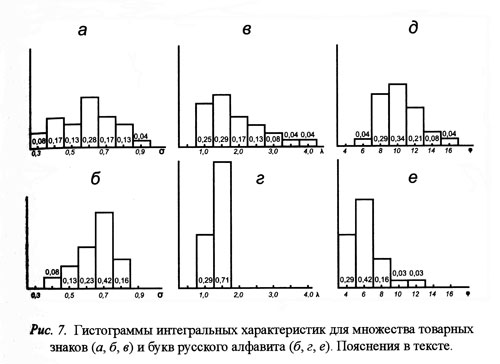
На рис 7, а и б приведены гистограммы значений σ для этих двух классов объектов, на рис. 7, в и г — соответственные гистограммы для величины λ. Сравнение гистограмм показывает, что хотя объекты этих двух классов изображений заметно отличаются по сложности и разнообразию свооих элементов, положения максимумов на гистограммах либо совпадают, либо близки.
Интегральные характеристики второго рода могут быть определены после декомпозиции изображения на элементы. Рассмотрим примеры таких характеристик, определенных для контуров изображения. В линии контура имеются точки, в которых кривизна линии контура изменяется скачком: это точки сопряжения прямолинейного отрезка и дуги, двух дуг с разными знаками кривизны и точки сопряжения двух дуг с кривизной одного знака, но сильно отличающихся по величине кривизны. Назовем эти точки разбивающими (в соответствии с принципом декомпозиции непрерывного стимула и реакции). Этими точками контур будет разбит на конечное число прямолинейных отрезков и дуг (острые углы контура — тоже дуги большой кривизны).
Учитывая высокую информативность криволинейных отрезков, введем теперь интегральные характеристики на множестве криволинейных отрезков контура. В качестве первой характеристики примем кардинальное число этого множества N, в качестве второй — сумму абсолютных приращений угла наклона касательной, или, иначе, сумму абсолютных величин дуг контура
φ = ∑i |Δφi|
где Δφi — величина i-той дуги в угловых единицах. На рис. 7, д, е приведены гистограммы величины φ для уже рассматривавшихся двух классов объектов: русского алфавита и набора товарных знаков.
Важнейшей интегральной характеристикой объекта является разнообразие. Это понятие оказывается довольно емким и многогранным. Оно тесно связано также с другими интегральными характеристиками — регулярностью, сложностью и т. д. Поэтому содержательный и количественный анализ этого понятия представляет большой интерес.
Выделим в понятии разнообразия в качестве компонентов разнообразие состава и разнообразие структуры. Разнообразие состава будет определяться алфавитом и его распределением (относительными частотами букв). Разнообразие состава, в свою очередь, можно разделить на разнообразие элементов и частей.
Однако к анализу разнообразия в целом возможен и другой подход со стороны анализа ограничений, накладываемых на возможное разнообразие различными факторами: условием связности, заданием точки отсчета, физическими ограничениями, принципами гармоничности. Кроме этого, имеется ряд характеристик изображения, тесно связанных и, в известной степени, производных от разнообразия и регулярности: упорядоченность, сложность, однородность, неопределенность. Характеристики (меры) сложности и разнообразия не совпадают между собой. Сложность в большей степени, чем разнообразие, зависит от числа элементов и операций установления отношений между ними. Точно так же не совпадают меры разнообразия, неопределенности, однородности и упорядоченности. Так, для меры упорядоченности необходима точка отсчета, чего не нужно для меры разнообразия. Меры упорядоченности не должны зависеть от числа элементов. Система может быть упорядоченной, но не однородной (443311) и может быть локально упорядоченной и однородной (431431).
Анализ разнообразия тесно связан с характеристиками отражателя и способом его взаимодействия с объектом. Существенными характеристиками отражателя являются его энтропия, емкость памяти и вид выполняемого им преобразования. Способы взаимодействия можно разделить на последовательные и параллельные, которые зависят от относительной величины объекта.
Подводя итоги, можно сказать, что на основе системы понятий: целое, декомпозиция, элемент, признак, алфавит, состав, отношение, множество отношений, структура, интегральная характеристика можно произвести полное аналитико-синтетическое исследование изображения как целого. Существенной особенностью этого пути является то, что он начинается от топологии (элемент), переходит к тополого-метрическому понятию (признак), затем к метрике, а затем опять к метрико-топологии (интеграл отношений) и снова к топологии. Этот путь показывает ведущую роль топологии и подчиненность метрики, что и логично, так как метрические пространства являются частным случаем топологических.
Выше были приведены некоторые примеры интегральных характеристик двуградационных изображений. В следующем параграфе будут описаны интегральные характеристики мелодий. В связи с интегральными характеристиками представляют интерес следующие вопросы:
Набор значений интегральных характеристик конкретного объекта отражает его индивидуальность в соответствующем классе объектов.
Гармоничный анализ объектов восприятия. Простейшим объектом, в котором реализованы все принципы гармоничного целого, является отрезок, разделенный на две части в золотом отношении. Рассмотрим теперь реализацию этих принципов в двумерных изображениях.
Повторение целого в частях означает, что один из признаков целого должен иметь близкие значения во всех ограниченных частях плоскости. Например, все части целого имеют близкую форму или колорит, ориентацию или эксцентриситет. Отсюда видно, что этот принцип реализуется на уровне состава. С точки зрения множества векторов, характеризующих части целого, это означает, что по одному из компонентов векторы сильно сближены.
Соподчиненность частей в целом применительно к изображению означает, что все части, во-первых, распадаются на три группы — главную, второстепенную и дополнительную, которые, в свою очередь, могут делиться. Основанием для такого распределения являются величины одного из признаков частей. В отличие от принципа повторения одного целого в частях, значения признака, по которому происходит соподчинение, должны занимать весь диапазон своих значений, располагаясь в нем по определенному закону. В качестве такого признака могут выступать положение в пространстве, величина, яркость, оптическая масса и другие. Соподчиненность реализуется на уровне структуры.
Множество метрических отношений объекта должно быть упорядочено в единую систему. Это достигается путем наложения ограниченной соразмерности. В объектах зрительного восприятия членение в каждом измерении производится по наиболее важным, фиксированным точкам. В случае двумерных объектов восприятия соразмерность может производится по каждому измерению в соответствии с применяемой системой координат. Рассмотрим в качестве примера изображение человека (рис. 8). Из рисунка видно, что функционально значимые и визуально фиксируемые точки тела, расположенные на вертикальной оси человека, связаны между собой метрическим (7—7—7—7—7), арифметическим (5—10—15) и геометрическим (7—11—18) рядами. Все размеры частей оси и вся ось имеют общий модуль. Этот, хотя и частный, но очень важный пример, а также анализ классических произведений живописи и архитектуры, позволяют высказать ряд соображений о соразмерности правильно (оптимально) организованных объектов зрительного восприятия.
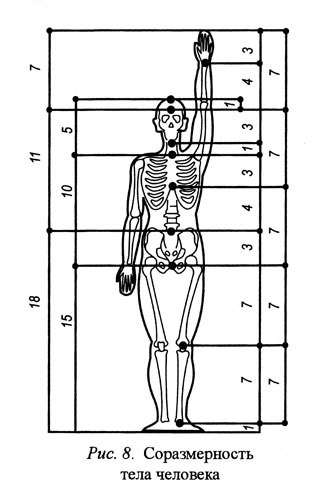
Важнейшие фиксированные точки объекта восприятия должны быть охвачены тремя видами закономерностей: метрическим, арифметическим и геометрическим рядами, причем каждый из рядов может проходить по несовпадающим точкам. Часто арифметический ряд совпадает с отрезком натурального ряда, а геометрический имеет своим знаменателем (динамическим модулем) величины √2, √3 и 0,5(√5 - 1) (золотое сечение).
В сложных объектах могут существовать несколько однотипных рядов, но с разными постоянными. Ряды могут охватывать часть объекта. Особенно часто общим закономерностям не подчиняются краевые элементы, служащие для согласования с окружающей средой или фоном. Благодаря этому в объекте, наряду, с детерминизмом метрических отношений, реализуется и элемент стохастичности, неопределенности. Каждый из трех рядов выполняет свою функцию: метрический ряд обеспечивает статику восприятия, геометрический — динамику, а арифметический — непрерывный переход от статики к динамике.
Схему метрических отношений тела человека (рис. 8) будем рассматривать как общий инвариант. Описание метрических отношений тела конкретного человека можно представить как отклонение от этого общего инварианта в относительных единицах. Тем самым будут разнесены регулярная и вариантная части описания.
Наличие в объектах восприятия и результатах репродуктивной деятельности (см. § 5 этой главы) регулярных метрических отношений, благоприятное воздействие таких отношений на запоминание, восприятие и движение позволяет поставить вопрос о механизмах, фиксирующих такие отношения.
Выделим ряд факторов, определяющих субъективное чувство равновесия: равновесие объекта относительно вертикальной и горизонтальной осей, уравновешенность направленных частей объекта, тональное равновесие. Равновесие объекта относительно вертикальной оси зависит от распределения оптических масс, положения главного элемента [68].
Из огромного многообразия звуковых стимулов, воспринимаемых человеком, выберем для анализа следующие элементы музыкального произведения: музыкальный звук, аккорд и мелодию. Такой выбор обусловлен следующим. Среди слуховых стимулов музыкальные произведения и его элементы обладают наибольшей регулярностью, регистрируемостью и удобны для исследования. Музыкальное произведение создается и воспринимается почти исключительно человеком. В силу этого оно неизбежно отражает как физические и физиологические свойства слуховой системы, так и психические процессы и состояния человека (включая и их социальный аспект). Музыкальное произведение представляет собой целостный объект, и в нем могут быть выделены относительно самостоятельные, устойчивые элементы, которые могут рассматриваться как целостные образования.
Говоря об устойчивости элементов и форм музыки, мы имеем в виду их пространственно-временную устойчивость, т. е. их инвариантность и распространенность в течение длительного времени и распространенность одних и тех же элементов и форм у разных народов земного шара. Вот что пишет по этому поводу Ю. Н. Тюлин: «...реалистическая музыка опирается на определенные основные нормы музыкального восприятия и мышления, имеющие общее значение для разных стилей. Эти нормы обладают большой исторической устойчивостью и сохраняют свое значение на протяжении многих столетий» [69]. И далее: «... в народной музыке разных национальностей при всем ее неисчислимом многообразии лады имеют определенные общие черты» [70].
Музыкальный звук как целое. Элементарным музыкальным стимулом является непрерывный чистый тон постоянной высоты и громкости и ограниченной длительности. Как и любой другой элементарный стимул, чистый тон характеризуется неразрывным единством временных, пространственных и энергетических характеристик. Его аналитическое представление имеет вид:
x = α sin ωt, 0 ≤ t ≤ τ,
где α — амплитуда; ω — частота; τ — длительность звучания. Чистый тон как ритмический процесс приятнее шума, однако, в силу большого постоянства своих параметров, он обладает недостаточным разнообразием. Музыкальный звук существенно отличается от чистого тона и других звуковых стимулов как объективно, так и субъективно. Известно, что музыкальный звук имеет сложную структуру и состоит из совокупности основного тона и обертонов, кратных основному тону. Музыкальные звуки, издаваемые одномерными (струны, воздушные столбы) и двумерными (стержни, пластины, мембраны) колеблющимися телами, существенно различаются по своему спектру: обертоны струн и воздушных столбов кратны основному тону, обертоны пластин, стержней, колоколов, человеческого голоса не кратны основному тону.
Музыкальный звук задается основным тоном, числом, высотой и интенсивностью обертонов. Но, кроме дискретных, музыкальный звук имеет и непрерывные компоненты. Основной тон — самый низкий по высоте и самый большой по интенсивности. Способ возбуждения звучащего тела, высота звука, индивидуальные особенности инструмента влияют на состав и интенсивность обертонов. Изменение спектра звука влияет на субъективную оценку звука. Увеличение числа обертонов в звуке превращает его в шум. Удаление некоторых обертонов изменяет тембр звука. Характеристики музыкальных звуков, издаваемых различными объектами, приведены на рис. 9 [71]. Рассмотрим эти данные с точки зрения общих характеристик целостности и гармоничности.
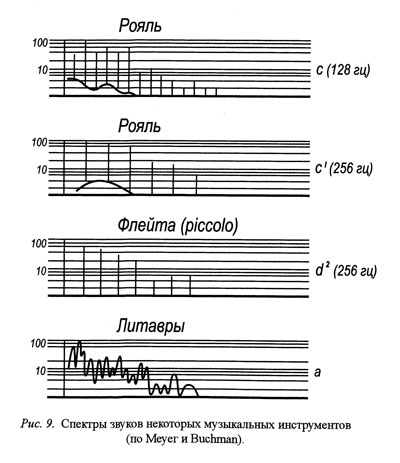
Связность основного тона и обертонов обеспечивается, во-первых, благодаря наличию непрерывного компонента, а во-вторых, квазисвязностью обертонов (за исключением высоких звуков). Спектр музыкального звука ограничен. Сходство дискретных компонентов состоит в октавном повторении основного тона. Основной тон и обертоны в основном упорядочены по энергии. Частоты обертонов кратны основному тону. Кроме частотной структуры может быть проанализирована и динамика звука.
Аккорд как целое. Современные теоретики музыки выделяют в ней три компонента: гармонический, мелодический и динамический. Аккорд как частный случай созвучия является одной из важнейших характеристик ладагармонической системы. «Аккорд, — по определению Тюлина, — представляет собой гармоническое единство, конструктивное целое, содержащее от 3 до 6 тонов» [72]. Аккорды имеют терцовое строение. «Только терцовое наслоение тонов придает звучанию особую компактность и выпуклость» [73]. В функциональном отношении аккорды делятся на мажорные и минорные, устойчивые (вызывающие состояние покоя) и неустойчивые (вызывающие ожидание движения). Примером устойчивого аккорда является тоническое трезвучие, неустойчивого — уменьшенный септаккорд. Звуки в аккорде должны консонировать с основным тоном и между собой. При объединении звуков в аккорд имеют значение не только основные тоны звуков, но и обертоны.
Структура аккорда определяется интервальными расстояниями между звуками. Существует четыре основных типа аккордов, построенных по терцовым интервалам (табл. 1.). При интервалах, меньших терции, возникают сильные биения. При интервалах, равных и больших терции, биения становятся слабыми. При интервалах, значительно превышающих терцию, уменьшаются различия между консонансом и диссонансом. На рис. 10 дано графическое представление ряда аккордов в логарифмических шкалах. Цифрами обозначены интервалы в полутонах между звуками аккорда. На рисунке отчетливо видно различие между терцовыми (рис. 10, б, в, г, д) и нетерцовыми (рис. 10, а, е) аккордами.

Рассмотрим теперь аккорды с точки зрения общих условий целостности и гармоничности. Аккорд состоит из звуков, его структура определяется звуковысотными отношениями. Между звуками имеется сходство по тембру, соподчинение (доминирует самый низкий звук), высоты основных тонов и части обертонов соразмерены. Связность обеспечивается одновременностью звучания всех звуков аккорда, близостью их во времени и по тембру.
Мелодия как целое. Мелодия, выделенная из текста музыкального произведения, обладает известной самостоятельностью, выразительностью, чертами органического целого. Б. В. Асафьев говорил, что мелодия — это душа музыки. Мелодия отражает мелодический и динамический компоненты музыки.
Она выражает и общие закономерности музыки, и наиболее индивидуальные, присущие именно данному музыкальному произведению. Среди трех компонентов (мелодия, гармония, ритмика) мелодии принадлежит ведущее значение.
Главную роль в мелодии играют высотные и временные отношения. В мелодии, как и в изображении, состав элементов имеет два уровня: уровень звуков и уровень интервалов. Они соответствуют областям и границам областей изображения. Мелодия делится на периоды и фразы. Отношения между ними определяют структуру мелодии. Различают масштабную, ритмичную и звуковысотную структуры мелодии.
Мелодию можно рассматривать как упорядоченную последовательность музыкальных звуков, каждый из которых характеризуется высотой h, длительностью l и громкостью g. Упорядоченную последовательность этих величин можно рассматривать как вектор M(h, l, g). Тогда мелодия описывается векторной функцией времени. Высота и длительность звуков изменяются, как правило, дискретно, громкость может изменяться и дискретно, и непрерывно. Функция M{t} дискретизируется в моменты времени, когда один или несколько компонентов вектора М изменяются скачками. Эти моменты и являются временными границами звуков. Такая функция может рассматриваться как модель мелодии с учетом тех ограничений, которые накладываются на эту функцию общими законами музыки.
Алфавитом мелодии является набор звуков, включая и пустой интервал. Мелодия представляет связную (или квазисвязную) и ограниченную последовательность звуков.
Проанализируем мелодию с позиций целостности и гармоничности. Для анализа по основным характеристикам целостности произведем изучение состава, временной и звуковысотной структуры и интегральных характеристик мелодий некоторого класса. На множестве элементов мелодии могут быть определены различные статистические характеристики. Как и в случае изображения, эти характеристики не определяют целостности мелодии, но их статистические распределения представляют определенный интерес. 0дна из таких характеристик связана с распределением устойчивых и неустойчивых звуков. Устойчивыми звуками в определенном ладу называются звуки, которые производят впечатление законченности, не требуют продолжения (разрешения). Объективность этого качества показана Беляевой-Экземплярской (1929). Устойчивых звуков в ладу три — тоника, 3-я и 5-я ступени. Наиболее устойчивой является тоника. Назовем ее абсолютно устойчивой, а 3-ю и 5-ю ступени — относительно устойчивыми. Неустойчивые звуки можно разделить по степени их тяготения к разрешению на более неустойчивые (до разрешения — полутон), менее неустойчивые (до разрешения — целый тон). Если приписать абсолютно устойчивой ступени значение + 1, относительно устойчивой — (+ ½), менее неустойчивой — (- ½) и более неустойчивой — (- 1), то получим следующее распределение характеристик устойчивости ступеней в ладах:
В мажоре: + 1, - ½, + ½, - 1, + ½, - ½, - 1, + 1. В миноре (натуральном): + 1, - 1, + ½, - ½, - 1, + ½, + 1. В миноре (гармоническом): + 1, + 1, + ½, - ½, - 1, - ½, - 1.
В соответствии с этой классификацией было определено процентное содержание нот с различными характеристиками. На рис. 11, а приведена гистограмма устойчивых звуков для мелодии «Детского альбома» П. И. Чайковского.

Состав частей мелодии и ее структура определяются принципом декомпозиции и типом рассматриваемых отношений. В мелодии обнаруживаются отношения порядка, толерантности, метрики и симметрии. Эти отношения определяют два основных типа структуры мелодии — ритмическую и мелодическую. Для мелодий существует также оптимальный уровень разнообразия, определяющий в значительной степени ее целостность. Очень часто повторность ритмов сопровождается повторностью мелодий.
Приемы повторений:
Также интересно проследить, существуют ли какие-то отношения между ритмическим и мелодическим разнообразием и между мелодическим разнообразием и количеством устойчивых звуков в произведении (так как отдельно повторяемый звук чаще всего является устойчивым).
В табл. 2 приведены оценки звуковысотного и ритмического разнообразия для мелодий «Детского альбома». Для оценки использовался коэффициент разнообразия ri (см. § 3 гл. II). За элемент принимался один такт. Тактовый уровень принимался за нижний уровень иерархии. Вторым был уровень предложений, третьим — уровень периодов, четвертым — уровень самой мелодии. На рис. 11, б и 11, в соответственно приведены гистограммы коэффициентов разнообразия rh и rt по данным табл. 2.
Эти данные показывают, что разнообразие по временным характеристикам почти всегда меньше, чем по звуковысотным, диапазон коэффициентов временного разнообразия уже, чем диапазон значений звуковысотного разнообразия (для данной выборки). Коэффициенты rh 22-х из 24-х мелодий лежат в интервале (0,35—0,65).
Мелодию можно рассматривать как частный случай текста. Поэтому ее структуру и разнообразие целесообразно сравнить с соответствующими характеристиками стихотворного и прозаического текста.
Особым сугубо человеческим объектом восприятия является текст. По сравнению с объектами, рассмотренными выше, текст обладает рядом особенностей. Он воспринимается сукцессивно, может восприниматься и зрением, и слухом. Он является универсальным способом отображения, представления информации, всех ее компонентов. Текст удобен для объективного анализа, в этом случае относительно просто решаются вопросы определения алфавита и состава. Текст относится к сигналам второго рода.
Текст в целом и его компоненты являются носителями смыслового значения, между компонентами текста, наряду с другими, действуют и семантические связи, играющие в структуре «текст» ведущую роль. Текст как целое интересен и в том отношении, что его составляющие также являются целыми единицами, здесь мы имеем дело с иерархией уровней целого: буква — слово — предложение — текст. Говоря о компонентах текста, можно отметить одну интересную особенность: помимо связных и ограниченных элементов состава имеются и неограниченные, занимающие промежуточное положение между целостными элементами: буква — слог — слово — синтагма (группа слов) — предложение — абзац — текст. Слоги, синтагмы, абзацы имеют открытые связи.
Текст и его части изучаются различными науками: лингвистикой, логикой, психологией. Лингвистика рассматривает вопросы синтаксиса и семантики текста, логика — вопросы структуры, связанные с актами мышления. Эти проблемы неразрывно связаны и с вопросами восприятия и усвоения текста, его воздействия на воспринимающего. Синтаксические, семантические, эстетические и прагматические характеристики текста определяют и его целостность.
Исходным элементом текста является знак. Знаки разделяются на основные (буквы алфавита, включая интервал для разделения слов) и вспомогательные (знаки препинания, кавычки, скобки, большой интервал для разделения абзацев и любые другие знаки). Но в зависимости от целей исследования в качестве элемента может приниматься не знак, а слово или предложение.
Состав элементов текста можно рассматривать как множество знаков (основных и вспомогательных) или множество слов. Как и ранее, состав текста можно характеризовать распределениями алфавитов данного текста и сравнением этих распределений с соответствующими распределениями языка.
Структурной единицей текста как целого является предложение. Частями предложения являются слова. Между словами в предложении имеют место синтаксические отношения следования, управления, согласования, однородности и вхождения в составляющие [74]. На основе этих отношений структура предложения может быть представлена в виде ориентированного графа (дерева). Дерево графа несимметрично, с более сильным ветвлением вправо, это отражает свойства языка. Глубина дерева ограничена, что, согласно гипотезе В. Ингве, обусловлено свойствами памяти человека. Предложение — грамматическая форма суждения. Элементы предложения и суждения не совпадают. Предложение имеет субъектно-предикатную структуру.
Текст — сложный объект. В нем можно выделить различные типы структур — логическую, синтаксическую, семантическую, временную. Но синтаксические связи действуют в основном внутри предложения. Связь предложений в целостную последовательность осуществляется главным образом с помощью семантических связей.
В структуре текста семантические связи имеют больший удельный вес, чем в структуре предложения (по сравнению с синтаксическими). Текст состоит из группы предложений и обладает определенной семантической обособленностью и присущими ему структурными закономерностями. Собственно и членение текста на абзацы производится в местах изменения смысла, и в этом отношении текст подчиняется общему правилу квантования целого. Для получения семантического компонента структуры абзаца в работе И. П. Севбо [75] предлагается следующий метод. Текст приводится к набору упрощенных стандартизированных предложений, устанавливаются типы отношений между этими элементарными предложениями. Ими оказываются отношения порядка и толерантности (автор использует другую терминологию). Выделяются лексико-семантические связи, основанные на повторяемости семантически близких понятий в тексте (синонимы и слова-заместители). Эти повторения автор называет нанизыванием. Затем выявляются схемы нанизываний. Далее автор рассматривает структуру текста только на основе нанизываний, отвлекаясь от других видов связей. И. П. Севбо вводит также локальные количественные оценки синтаксической и семантической близости (число одинаковых слов в двух связанных предложениях — степень сцепления, степень удаленности слов-заместителей).
Однако, как отмечает автор, нанизывание является только одним из способов организации связного текста. Связь может осуществляться с помощью семантически близких понятий или общности ситуации. Объединение может происходить на основе принадлежности слов к единой семантической группе (виды одного рода). Общность ситуации может основывается на одном и том же отрезке времени или пространства (пейзажные описания).
Л. П. Доблаев [76] рассматривает текст без разбиения его на абзацы, элементом текста считается предложение, которое рассматривается как субъектно-предикатная структура суждения. Автор показывает, что и текст в целом также имеет аналогичную двухчастную структуру, имеет текстовый субъект, текстовый предикат, выражающие текстовое суждение. Текстовый субъект выражается чаще в одном предложении, а предикат и суждение — в нескольких. Интересно, что те же соотношения обнаруживаются в предложении: предикатная группа слов, как правило, более многочисленна, чем субъектная.
Наличие аналогии между текстом и предложением является основанием для выбора предложений в качестве частей текста как целого. Подобно тому, как основной смысл предложения может быть выражен в его субъектно-предикатной группе, основной смысл абзаца (и текста в целом) может быть выражен одним предложением.
Интересно, с нашей точки зрения, сравнить между собой три вида текстов: прозаический, стихотворный и мелодию, рассматриваемую как текст, Сравним эти тексты по ряду характеристик и посмотрим, как эти характеристики меняются от текста к тексту. В качестве характеристик используем типы отношений между компонентами семантической и метрической структуры. Метрической (временной) структурой назовем такую, которая получается в результате естественного разбиения текста на непересекающиеся части. Эта структура аналогична пространственной структуре изображения. Для каждого из рассматриваемых текстов эта структура имеет несколько иерархических уровней. В прозаическом тексте это текст — абзац — предложение, в стихотворном это стих — строфа — строка — стопа, в мелодии это — сама мелодия — период — фраза — такт. В прозаическом тексте эта структура в основном совпадает с семантической, так как абзац и предложение являются единицами семантической информации. Но при переходе от прозы к мелодии это соответствие все более нарушается, временная структура становится все более жесткой метризованной, уменьшается значение отношений порядка, увеличивается роль отношений толерантности, уменьшается смысловая нагрузка текста и увеличивается эмоциональная. Изменяется характер информации, передаваемой текстом, — от логической к образной.
Таким образом, в рассматриваемых текстах имеются две основные структуры — временная (метрическая) и семантическая. В прозаическом тексте доминирует семантическая структура, в мелодии — метрическая, в стихе могут доминировать и метрическая, и семантическая. Варьируя степень сходства и порядка компонентов текста, можно получать различные величины разнообразия и регулярности текстов.
Рассматривая восприятие как отображение предметов и явлений внешнего мира в субъективном пространстве, целесообразно сопоставить этот процесс с отображением другого типа, в известной степени обратным — отображением субъективного образа в двигательном акте. Оба этих отображения o рассматриваться как информационные процессы и должны иметь определенное сходство.
Можно выделить две неразрывно связанные стороны двигательного акта: внутреннюю и внешнюю. Наиболее полное исследование двигательного акта как целого было проделано Н. А. Бернштейном. В классической работе «О построении движений» он обосновал представление об иерархической многоуровневой системе построения движений. Уже в более поздних исследованиях Н. А. Бернштейн пришел к выводу о регулирующей роли образа в построении движений.
Внешняя сторона двигательного акта всегда представляет собой единство пространственно-временных и энергетических характеристик. В случае произвольного двигательного акта к ним добавляются еще и информационные характеристики. Элементарный непроизвольный двигательный акт вполне аналогичен ощущению — оба имеют одни и те же топологические характеристики и неразрывное единство пространства, времени и энергии. Далее, если составной частью восприятия всегда является действие, то составной частью двигательного акта всегда является рецепция. И восприятие, и двигательный акт имеют в своем составе замкнутые контуры регулирования.
Двигательные акты можно разделить на произвольные и непроизвольные, апериодические (однократные) и периодические (повторяющиеся), простые и сложные. В каждом двигательном акте представлены осознаваемые и неосознаваемые компоненты. В иерархии управляющих уровней осознаются лишь высшие.
Внешний компонент движения может изучаться либо непосредственно, либо по пространственно-энергетическим зависимостям от времени, зарегистрированным приборами. Больший интерес представляют информативные движения. Вспоминая «человека» Пенфилда, сразу можно сказать, что наиболее информативными движениями обладают лицо, язык и рука.
Произвольный двигательный акт есть целостное действие, результат которого может быть объективно зафиксирован. Так как такой результат является отображением субъективного образа, то интересно подвергнуть его такому же анализу, какому были подвергнуты объекты восприятия. Одним из наиболее информативных органов человека является рука, поэтому в качестве объектов анализа можно выбрать двигательные акты руки, а именно движение руки при письме, точнее результат таких движений — траекторию пишущего прибора.
Как большинство производственных движений, акт письма относится к периодическим движениям. Существует непосредственная связь между организацией двигательного акта и его эффективностью. Хорошая организация двигательного акта должна удовлетворять принципам гармоничности (трудовая деятельность).
В качестве конкретного объекта рассмотрим движения конца пишущего прибора. Его траектория соответствует начертаниям рукописных букв и слов. Она является объектом зрительного восприятия и контроля, результатом работы многоуровневой системы построения движения (отображения II). Ее исследование проведем методом «анализа через синтез».
Рассмотрим способ синтеза рукописных букв и слов. При разработке способа ставилась задача получения максимального сходства синтезированных букв из достаточно большого алфавита со стандартным, общепринятым их написанием при минимальном числе составляющих элементов. Известны различные подходы к решению этой задачи. Можно, например, получить конфигурацию буквы из элементов формы. Конфигурация, полученная в результате письма, есть результат движения. Поэтому в качестве элементов для синтеза рукописных букв естественно попытаться использовать простейшие типы движения. Будем считать, что конец пишущего прибора одновременно может участвовать в трех независимых движениях:
u = A sin [ 2π / (T × t) + φ1 ];2) прямолинейном колебательном под углом к горизонтали:
v = B sin [ 2π / (T × t) + φ2 ];3) прямолинейном поступательном по горизонтали:
w = C t.
Все движения происходят в одной плоскости. Для такого предположения имеются весьма убедительные физиологические данные. Результирующее движение полностью определено, если задать начальное положение пишущего прибора, амплитуды колебаний (А и В), период Т, разность фаз Δφ = φ1 - φ2 и скорость поступающего движения С. При различных значениях этих параметров получаются варианты эллиптической траектории как результат суперпозиции трех движений u, v и w.
Рассмотрим процесс синтеза рукописной строчной буквы а. Написание буквы а может быть произведено без отрыва пишущего прибора от бумаги. При этом некоторые участки конфигурации буквы могут проходиться неоднократно. Разобьем эту непрерывную траекторию на отдельные участки, показанные на рис. 12, а. Эти участки представляют собой эллипс, отрезок прямой и часть эллипса. Каждый из этих участков получается при различных комбинациях значений параметров А, В, Δφ, С, которые должны изменяться при переходе от одного участка к другому. Их можно рассматривать как некоторые функции времени А(t), B(t), Δφ(t) и С(t). На рис. 12, б даны графики этих функций при синтезе буквы а на интервале 0 ≤ t ≤ 2Т.
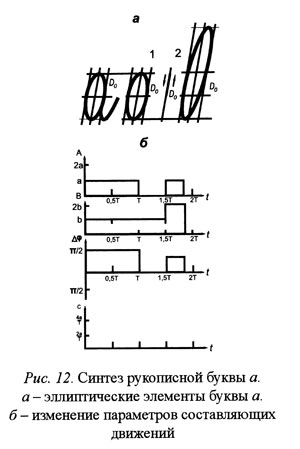
На графиках отчетливо видно, что разбивающие точки на траектории движения соответствуют моментам времени, в которые происходит скачкообразное изменение, по крайней мере, одной из четырех функций. Этот принцип разбиения непрерывной траектории движения на отдельные участки аналогичен тому, который был применен выше для квантования объектов восприятия. Аналогично можно синтезировать все строчные буквы русского алфавита [77].
На рис. 13 приведены конфигурации синтезированных букв, на этом же рисунке для сравнения приведены общепринятые начертания тех же букв. Сравнение показывает, что, за небольшими исключениями, для сходства синтезированных и стандартных букв необходимо очень небольшое число значений параметров: для А — 4, для В — 4, для Δφ — 7, для С — 3, причем эти значения оказались кратными, имеющими простую общую меру. Шкала времени также оказалась разбитой на дискретные интервалы с единицей, равной 1/12 T (периода). Подобно тому, как мелодия имеет ритмовысотную метрическую основу, движения при письме, по-видимому, имеют пространственно-временную метрическую основу.

Синтезированные буквы сравнивались с прописями, т. е. не с движениями отдельного человека, а с некоторыми усредненными начертаниями. Поэтому в реальных движениях могут быть и всегда имеются отступления от идеальной пространственно-временной основы. При тех же уровнях квантования можно синтезировать и строчные буквы латинского алфавита. При написании прописных букв траектория часто не является непрерывной, состоит из нескольких отдельных частей. Все такие части прописных букв русского и латинского алфавитов могут быть синтезированы описанным методом при некотором расширении числа уровней квантования начальных условий и параметров движения. Могут быть получены варианты букв, отличающихся наклоном, эксцентриситетом (вытянутостью) и размером.
Для многих букв алфавита выбор начальных условий и значений параметров движения не является однозначным. При незначительных вариациях этих величин могут быть получены различные, но близкие начертания букв, из которых могут быть выбраны в некоторых отношениях лучшие варианты. В частности, наиболее вариативны соединительные элементы букв. Характер соединительных элементов, которые у рукописных букв русского алфавита в основном завершают написание буквы, определяется последующей буквой слова. Варьируя эти элементы, а также вводя движение, прерывающее линию письма, можно осуществить программирование написания целых слов и предложений. Следовательно, программирование написания рукописного слова может быть осуществлено с помощью синхронного задания нескольких ступенчатых функций дискретного аргумента.
Таким образом, траектория движения при письме является квазисвязной и частично ограниченной, имеет «кристаллическую» пространственно-временную основу. Ее структуры во многом аналогичны структурам рассмотренных выше текстов.