Будем называть объект восприятия целым, если он обладает связностью (целое суть одно). Для объектов чувственного восприятия это, прежде всего, связность в пространстве и времени. Накладывая дополнительные ограничения (ограниченность, степень связи с внешней средой, полнота набора составляющих и т. д.), можно получить частные случаи целого. Такому определению удовлетворяют любые отдельные сущности, могущие быть объектами восприятия. Геометрически такому определению соответствует любая связная область в пространстве соответствующего числа измерений. Связность — ведущий признак целого. Он применим к любым целым: к целому — элементу и целому — системе, ко всем целостным объектам природы, включая Вселенную. Понятие связности позволяет дать и числовую характеристику целого: целое суть одно, независимо от того, является ли целое элементом или образовано единством многообразия элементов системы. Различие по мере связности позволяет выделять более связаные объекты в менее связной среде.
Иногда в качестве признака целого предлагается признак сохраняемости, инвариантности во времени. Но что сохраняется? Прежде всего, связность, затем ограниченность. Эти свойства и должны сохраняться при изменении целого, именно они являются главными инвариантами целого. Иногда в качестве признака целого рассматривается устойчивость. Однако объект может быть целым, но функционально неустойчивым.
Заметим, что приведенное выше определение целостного объекта является относительным. Все объекты являются относительно целыми, ибо все они в той или иной степени связаны с окружающей средой. «Универсальными частями любого материального объекта можно считать совокупность внутрисистемных и внесистемных связей» [39]. Эти связи находятся в отношении дополнительности. В предельном идеальном случае, когда весь объект «замкнут» в себя, т. е. когда внешние связи отсутствуют, можно говорить, как предлагает Г. П. Короткова, об идеальном целом.
Представим себе линейную шкалу целостности, нормированную к единице. Точка «0» соответствует граничному переходу нецелое-целое, точка «1» — идеальному целому. Границы отрезка — точки «0» и «1» — это точки, в которых целое перестает существовать. В обоих случаях это происходит из-за нарушения основного свойства целого — его связности. Однако эти границы качественно различны: в точке «0» нарушается связность между частями целого (целое распадается на части, становится нецелым), в точке «1» разрушаются связи целого со средой, целое исключается из среды и гибнет. На границах интервала (0—1) целое перестает существовать, т.е. происходит разрыв непрерывности времени существования. Факт связности объекта при отражении зависит и от свойств (разрешающей способности и чувствительности) отражающей системы. Для систем с различной разрешающей способностью один и тот же объект может быть определен и как связный, и как несвязный. Для снятия этой неопределенности необходимо задать нижнюю границу чувствительности (связь уже есть) и верхнюю границу разрешающей способности (разрыва еще нет). Но эти пороги, в свою очередь, будут зависеть от свойств объекта. Определяющим фактором при этом являются относительные размеры частей и разрывов. В основу классификации целостных объектов могут быть положены признаки объекта и его связей со средой, а также признаки отражающей системы.
Существуют два основных пути изменения целого, которые имеют место как на фазе генеза, развития, эволюции, так и на фазе деструкции, распада, инволюции целого — путь интеграции и путь дифференциации. В обоих случаях происходит изменение связности целого. Степень связности сильно изменяет все свойства целого. Эволюция динамического целого происходит, как правило, в направлении увеличения связности. Слабая связь дает большое комбинаторное богатство. Жесткие структуры обладают большей экономичностью, быстродействием, но малонадежны (выпадение одного звена может привести к разрушению). А. А. Малиновский показал [40], что в биосистемах имеет место чередование этих типов связности, чем и обеспечивается объединение достоинств обеих систем. В ряде работ У. Р. Эшби показал влияние связности частей мозга на приспособительную деятельность организма.
В зависимости от уровня знаний и задач, которые решает исследователь, целое может рассматриваться как элемент (далее неразложимый) или как система элементов или субсистем (частей целого). Целое как элемент может обладать рядом свойств или признаков, которые определяются его отношениями с окружающей средой (функцией целого). Этими же отношениями определяются и характеристики связности и ограниченности. С функциональной точки зрения элемент почти всегда может рассматриваться как преобразователь.
Части систем на любом уровне могут рассматриваться как элементы. Их внутренние устройства аккумулированы и выражены в общих свойствах этих частей как неразложимого целого. При таком подходе возможны ошибки лишь в том случае, если опущены существенные признаки элементов. Любое целое всегда является диалектическим единством противоположностей. Уже выделение диалектических пар в целом — элементе позволяет рассматривать его как систему. Определений понятия «система» существует великое множество, поэтому приведем лишь одно.
«Системой называется совокупность любым способом выделенных из остального мира реальных или воображаемых элементов. Эта совокупность является системой, если: 1) заданы связи, существующие между элементами; 2) каждый из элементов внутри системы считается неделимым; 3) с миром вне системы система взаимодействует как целое; 4) при эволюции во времени совокупность будет считаться одной системой, если между ее элементами в разные моменты времени можно провести однозначное соответствие» [41].
В целом, как системе, следует различать состав и структуру что делается далеко не всегда, и часто эти понятия смешиваются. Состав — это множество, набор элементов или частей, образующих целое. Характеристиками состава являются алфавит частей и характеристики распределения частей. Алфавит должен удовлетворять требованиям полноты. Проблема полноты применительно к целому имеет различные аспекты. Можно выделить полноту алфавита, полноту состава частей, полноту набора признаков целого.
Алфавит — это всегда набор классов, внутри которых элементы неотличимы, а число их бесконечно или очень велико. Полнота алфавита позволяет синтезировать любой объект из определенного множества. Алфавиты, как правило, ограничены. Так, алфавит химических элементов состоит из, немногим, более сотни элементов, буквенные алфавиты содержат десятки единиц, еще меньше цифровые алфавиты. Единицами измеряются алфавиты полных наборов булевых функций математической логики, алфавиты функциональных блоков аналоговых вычислительных машин (интегратор, сумматор, множительный блок, инвертор, генератор функций). Таким образом, и природа, и человек вполне обходятся небольшими алфавитами.
Наиболее важное значение характеристика полноты имеет по отношению к составу частей целого. Нарушение полноты состава частей в реальных целостных объектах приводит в лучшем случае к ухудшению функционирования, в худшем — к гибели объекта. Нарушение полноты отражения целого приводит к искажению представлений о целом. Прежде всего, полноту состава частей обеспечивают противоположные компоненты (целое как единство противоположностей). Полнота свойств целого означает перечисление всех основных (в данном отношении) свойств.
Определение состава целого связано с правилами его декомпозиции на части, с проблемой дискретизации непрерывного. Основными формами существования целого являются пространство и время. Поэтому квантование (декомпозиция) основывается, прежде всего, на дискретизации свойств объекта в пространстве и времени, на разрыве непрерывности одних свойств объекта при сохранении непрерывности других (в противном случае может нарушиться связность). Для декомпозиции сложного целого весьма существенным является наличие в нем различных временных и пространственных уровней (наборы различных постоянных времени, различных масштабов и т. д.).
Элементы объединяются в целое множеством отношений. Отношение является универсальной формой связи. Любое отношение предполагает сохраняющиеся свойства и ограничение возможных состояний соотносимых элементов или систем. Связь является частным случаем отношения при наличии движения или изменения. Отношения можно классифицировать как по признакам их элементов, так и по характеристикам самих отношений. По признакам элементов отношения можно разделить на временные, пространственные, энергетические, информационные и т.д. По характеристикам самих отношений — на детерминированные и вероятностные, на метрические, топологические, и логические, линейные и нелинейные, на структурные и функциональные.
Отношения могут отражать зависимость, близость, порядок множества элементов целого. Они могут существовать только между частями целого или как между частями, так и между частями и целым.
Система отношений в целом, как правило, является многоуровневой с четкой взаимосвязью между уровнями. Частным видом такой системы является иерархия. Под действием отношений (связей) элементы в составе целого могут утрачивать некоторые из своих свойств или, наоборот, приобретать новые.
Таким образом, в отличие от своих частей целое содержит не только эти части в качестве составляющих, но и отношения между ними. Так, алгоритм, полученный в качестве композиции других алгоритмов, содержит большее число шагов, чем его составляющие, за счет добавления связок между последними. С увеличением числа компонентов целого резко возрастает число отношений. Отношения обеспечивают целостность системы. Поэтому целое приобретает некоторые свойства, которыми не обладали его части, поэтому оно не является простой суммой своих частей. Кроме этого, свойства целого определяются не только внутренними отношениями, но и внешними отношениями целого со средой, которые также изменяются при объединении частей в систему. Добавление или исключение элементов изменяет свойство системы или даже разрушает ее. Эти операции (добавления или исключения) несимметричны по своим результатам.
Структура целого определяется совокупностью инвариантных отношений между элементами. Любая структура уменьшает число возможных независимых состояний.
Существует, как правило, более одного способа декомпозиции системы. Поэтому невозможно однозначно определить структуру системы до тех пор, пока не выбран тот или иной способ декомпозиции. Однако среди различных способов декомпозиции существуют такие, которые могут быть названы естественными. «Частями следует называть лишь такие взаимодействующие («вложенные») структуры, которые подчиняются тем же законам, что и целое, которые служат формой проявления этих законов» [42]. В работе М. Тоды и Э. X. Шуфорда [43] высказывается мысль о том, что в нашем мире существует громадное множество различных ситуаций, но, по-видимому, сравнительно небольшое число структур, и что все структуры должны иметь некоторые общие логические аспекты, будь то структура в физике, структура в психологии или социологии.
Но структура объекта определяется не только способом декомпозиции, но и типом отношений. А. С. Кравец выделяет следующие аспекты изучения структуры [44]: 1) пространственное расположение (субстанциональный подход), 2) организация (структура — совокупность функциональных блоков и связей между ними), 3) функциональный подход (при функциональном подходе под структурой понимают совокупность отношений между существенными переменными). Значимость переменных в целом неодинакова. Его состояние определяется в основном небольшим числом существенных переменных, а остальные описывают лишь малозначимые детали. Важное значение имеет также рассматриваемый интервал времени. Существенными являются те процессы, постоянные времени которых, соизмеримы с рассматриваемым интервалом времени.
Структура целого зависит от того, на каком этапе эволюции находится система, и, наоборот, зная структуру, можно предсказать, на какой фазе эволюции она находится. В филогенезе среда эволюционировала от гомогенности к гетерогенности. На определенном этапе она стала предметной, причем предмет воспринимался еще как целое. Но далее произошло структурирование уже внутри предмета. Параллельно с этим развивались и процессы восприятия — от восприятия целостных предметов и их отношений к восприятию частей предмета и их отношений, их структуры, т. е. наряду с процессами анализа развивались и процессы синтеза. Но примат всегда был за восприятием нерасчлененного целого, а потом уже происходил его синтез из частей.
Гомогенная среда (множество элементов) должна распадаться на подмножества таким образом, чтобы объем подмножества не превосходил некоторого предела, в противном случае само это подмножество должно также распасться. Эта закономерность обнаруживается на всех уровнях организации. Она является одной из причин того, что структура целого становится многоуровневой, иерархической.
Л. Берталанфи [45] выделяет следующие виды иерархий: разделительную (результат деления клеток), пространственную, генетическую (от яйца и далее во времени), морфологическую (от высших систем к познанию), физиологическую, сегрегационную (иерархия в результате дифференциации), интеграционную иерархию. В пространственной иерархии различаются пространственно локализуемые и отделимые компоненты и пространственно нелокализуемые и неразделимые компоненты. В структуре и функционировании иерархий любой природы обнаруживаются общие свойства.
Выше рассматривались преимущественно характеристики целого как системы, но все основные понятия остаются верными и по отношению к процессу. Процесс есть изменение, динамика целого во времени, которая является условием его существования. Главной особенностью процесса как целого является связность во времени. По критерию ограниченности все процессы можно разделить на незамкнутые во времени и замкнутые. Первые не имеют фиксированных границ во времени, вторые имеют начало и конец. В процессах этого типа всегда можно выделить три фазы: становление, стационарная фаза и инволюция. Фазы процесса представляют его состав. Понятие структуры процесса предполагает, что из всего множества отношений между частями целого ведущее значение отводится временным отношениям. Это, разумеется, не означает, что время отрывается от пространственных и иных отношений структуры. Важнейшими характеристиками любого процесса являются длительность его существования и длительности отдельных фаз. Именно эти временные признаки целого, его частей и отношения между ними и образуют структуру процесса. Точками разбиения непрерывного процесса на фазы являются моменты разрыва непрерывности отдельных характеристик процесса. Имеет место важная особенность связей между фазами процесса — их временная асимметрия. Предыдущие фазы влияют на последующие, но не наоборот. «Все последующие фазы развития человека преемственно связаны с предыдущими, причем не только с ближайшей, смежной, но и со всеми отдаленными, даже исходными, начиная с раннего детства» [46]. Любой процесс происходит в ограниченном пространстве. Поэтому его характеристиками могут являться не только динамика во времени и одномоментные пространственные «срезы». Продольные и поперечные срезы взаимно дополняют картину процесса как целого. Только в единстве системы и процесса, пространственного и временного описания целого, в единстве эволюции и гармонии можно получить наиболее адекватное отражение целого при доминировании пространственного или временного компонента.
Для каждой из двух форм целого (нерасчлененной и расчлененной) могут быть введены интегральные характеристики — качественные и количественные. Состав и структура этих характеристик отражают свойства целого. Набор качественных характеристик должен быть полным. Для количественныx характеристик должны быть введены меры и шкалы измерений, и в этих шкалах определены средние, граничные и оптимальные значения для заданных множеств целостных объектов или частей одного и того же объекта.
Для непрерывного, нерасчлененного целого качественными характеристиками являются характеристики связности, ограниченности и некоторые другие (см. § 3, гл. II). Для дискретных, расчлененных целых, кроме этого, могут быть введены и другие характеристики состава и структуры. Все рассматриваемые далее характеристики — одномерные. В соответствии с диалектической противоположностью целого их шкалы будут иметь характер дихотомических шкал. Помимо частных дихотомий любое целое обладает следующими неразрывно связанными полярными свойствами: дискретностью и непрерывностью, регулярностью и нерегулярностью, однообразием и разнообразием. Ведущей дихотомией является дихотомия один — много (в числовом выражении) или постоянство — изменение (в физическом выражении). Каждой дихотомии можно сопоставить числовую ось, нормировав ее длину к единице. Параметры объекта могут быть распределены или по всей оси, или на ограниченной ее части, или сосредоточены в отдельных точках. А целое, таким образом, можно характеризовать узлом таких, дихотомических осей.
Как уже отмечалось, целое не есть сумма своих частей. Поэтому и интегральные характеристики целого в общем случае не являются аддитивными функциями, хотя некоторые из характеристик и могут быть получены простым суммированием. Некоторые из характеристик целого являются нелинейными функциями характеристик частей. Например, характеристика целого может быть больше суммы своих частей (сверхаддитивное нелинейное сложение). Многие физические характеристики целого аддитивны (объемы, массы, силы, сигналы). Возможен и третий случай инфрааддитивного нелинейного сложения, когда результирующие меньше суммы составляющих. Примером может служить энтропия объединенной системы, если объединяемые подсистемы зависимы. Многие из интегральных характеристик целостных динамических систем являются регулируемыми, поддержание их в определенных границах есть условие их существования.
Интегральные характеристики целого могут быть независимыми от свойств, отражающей это целое, системы (объективными) и могут быть зависимы от свойств последней. Кроме того, следует различать объективные интегральные характеристики целого и особенности их отображения различными отражающими системами.
Анализ реальных целостных систем показывает, что всем им присуще разнообразие свойств частей. Более того, жизнеспособными оказываются лишь системы с определенным уровнем разнообразия. Так, в атоме нет двух электронов с одинаковыми квантовыми числами. Тройные, звезды с близкими компонентами «вымирают» (столкновение и взрыв). Н. В. Тимофеев-Ресовский, Ю. М. Свирежев и А. Д. Базыкин показали на математических моделях, что полиморфизм биосистем ведет к повышению их устойчивости. К такому же выводу приходит и К. Гробстайн: «Более высокие уровни организации биомассы не заменяют более низких, какими бы преимуществами ни обладали первые по сравнению со вторыми. Различные уровни сосуществуют в биомассе, обеспечивая ее многообразие, которое... является важнейшим фактором стратегии жизни в ее взаимоотношениях с изменяющейся средой» [47].
Разнообразие может быть реализовано или в структуре, или в процессе, или в том и другом одновременно. В сложных биологических системах имеет место разнообразие постоянных времени процессов регуляции, временных констант полураспада тканей и т. д. Уоддингтон в «Стратегии генов» отмечает, что «биологическая картина сложнее физической в основном по способу, каким в нее включается время» [48]. Иерархическое построение временной организации клетки было показано Кэксером.
У. Р. Эшби сформулировал закон необходимого разнообразия применительно к процессу регулирования. Аналогичную теорему предложил К. Шеннон по отношению к передаче сигналов по каналу с шумами. Структурное разнообразие систем, необходимый уровень этого разнообразия суть проявление этих закономерностей. По отношению к составу целого необходимое разнообразие частей является другим выражением условия полноты состава, обеспечивающего нормальное функционирование целого.
Отражение разнообразия объекта зависит от свойств отражающей системы. В теории информации показывается, что количество информации, получаемое отражающей системой, ограничено энтропией этой системы.
Близкими по смыслу являются дихотомии: регулярность — нерегулярность; упорядоченность — неупорядоченность; определенность — неопределенность. Вторая из дихотомий относится к пространству, третья — ко времени, а первая включает их обе как частные случаи. Определенное соотношение упорядоченности и неупорядоченности в целом является необходимым условием его существования. Полный порядок и полный беспорядок равносильны разрушению целого. Для каждого целого существует оптимальное соотношение порядка и беспорядка. Соотношение определенности — неопределенности проявляется на всех уровнях организации — от физического до социального. На микрофизическом уровне оно находит свое отражение в соотношении неопределенности. Л. Бриллюэн обратил внимание на то, что и на макрофизическом уровне действуют те же закономерности. Наличие определенности и неопределенности во внешней среде необходимым условием нормального состояния и деятельности человека. Правда, средняя величина оптимального соотношения определенности — неопределенности неодинакова для людей с разными типами нервной системы.
Регулярность и нерегулярность разнесены в пространстве и времени, или такое разнесение может быть сделано по пространственным и временным характеристикам. Разнесение во времени проявляется, в частности, в регулярности физических законов и нерегулярности (поскольку они не могут быть проконтролированы с любой точностью) начальных условий. Разделение регулярности и нерегулярности в физических закономерностях обнаруживается и по пространственным характеристикам: пространственные характеристики нерегулярностей, как правило, на макроуровне значительно меньше регулярных составляющих, например, нарушения симметрии весьма незначительны.
Для целостных систем на каждом уровне организации существует область допустимых и оптимальных значений регулярности и разнообразия, которые могут быть интерпретированы как проявление законов необходимой регулярности и разнообразия соответственно или как законы ограничения регулярности и разнообразия сверху и снизу.
Целое взаимодействует со средой как элемент большего целого. В этом взаимодействии главную роль играют уже не свойства его частей, а его интегральные характеристики. Среда (большее целое) также состоит из элементов (односвязных или многосвязных). Очень часто целое содержит многосвязные элементы, своего рода соединительную ткань. Связи «односвязное — односвязное» и «односвязное — многосвязное» существенно различны.
Положение целого в среде определяется, прежде всего, его пространственно-временными координатами. Причем в любом случае пространство и время оказываются неравноценными, одно из них всегда является ведущим. Далее отношение целого со средой определяется обменом (веществом, энергией, информацией). Системы различаются по составу компонентов обмена него интенсивности.
Взаимоотношение внешних и внутренних связей, как уже отмечалось, определяется принципом дополнительности. Однако на соотношение внешних и внутренних связей должны быть наложены ограничения. Внутренние связи должны преобладать над внешними, чтобы последние не могли разрушить целого. Кроме того, внутренние связи должны обеспечивать инвариантность существенных отношений внутри целого при взаимном относительном движении его частей. С другой стороны, преобладание внутренних связей над внешними не должно быть слишком большим, так как уменьшение удельного веса внешних связей приводит к изоляции объекта от среды, что в свою очередь может привести к его гибели. Таким образом, можно сделать вывод о том, что должна существовать оптимальная зона на шкале отношений внешних и внутренних связей, обеспечивающая наибольшую устойчивость целого в данной среде.
По основной характеристике целого — связности — можно выделить следующие уровни целостности: нецелое (несвязное), целое (связное), оптимально связное и единое целое (максимально связное). Критериями оптимальности целого могут служить и другие его характеристики — ограниченность, полнота и т.д. Все критерии качества целого относительны: с изменением условий (внешней среды) изменяется и критерий оптимальности. Попытки установить какие-то абсолютные характеристики качества целого, по-видимому, несостоятельны. Так, например, иногда говорят, что «целое это то, от чего ничего нельзя отнять и к чему ничего нельзя добавить». Однако в отношении избытка и недостатка в зависимости от уровня целого оно оказывается несимметричным. А. Сент-Экзюпери считал, что главный признак целого определяется невозможностью чего-нибудь отнять. Однако во многих случаях добавление также невозможно. Различные уровни целого обладают различной «чувствительностью» к изменениям. Возможно, например, что неудачи цветомузыки связаны с тем, что цвет пытались добавить к уже имеющимся целостным произведениям, а не к специальным, рассчитанным на бимодальное восприятие. Критерий экстремума часто используется в искусстве для характеристики оптимального целого: достичь многого малыми средствами, единства в многообразии и т. д.
Гармоничное целое — это своего рода идеальное целое, к которому в большей или меньшей степени приближаются реальные объекты, это своего рода инвариант целого. Поэтому гармоничность моноэкстремальна. Оптимальность же полиэкстремальна, оптимум может достигаться по различным критериям. Гармоничное может не совпадать с оптимальным в данных условиях, однако, все оптимальные решения (зона оптимальности) располагаются вокруг области (или точки) гармоничности (см. § 3, гл. IV). Гармоничные системы обладают повышенной устойчивостью (длительностью существования) во времени и способностью к большему распространению в пространстве, а также и более эффективному функционированию. В изменяющейся среде система не может быть гармоничной, если она не будет адаптироваться к изменившимся условиям. Требование устойчивости не противоречит свойству изменчивости. Наоборот, устойчивые системы обладают хорошей изменчивостью.
В ходе эволюции целостных систем можно отметить следующие три различные тенденции: 1) сохранение инвариантов; 2) колебательные изменения относительно средних значений; 3) поступательное изменение. Так, в биологических системах асимметрия возрастает по эволюционной лестнице от полной симметрии некоторых растений и простейших животных до полной асимметрии (речевой центр в левой половине мозга). Те же закономерности обнаруживаются и в описывающих языках. Поступательные изменения происходят в музыке, архитектуре, поэзии и т. д. Эти изменения происходят в направлении отклонения от правильности, порядка, в сторону аритмии и асимметрии. М. Гика писал: «По прошествии фазы прямоугольного пуризма, вероятно, произойдут криволинейные реакции морфологического и даже архитектурного динамизма. Колебания между аскетизмом и жизнерадостностью, между сдержанностью и экспансивностью, часто проявляющиеся в душевном состоянии индивидуумов, всегда сопровождали художественные, интеллектуальные и религиозные проявления народов или отдельных ветвей человечества, объединенных общей цивилизацией» [49].
С древнейших времен и до наших дней философы, естествоиспытатели и художники использовали понятие гармонии, вкладывая в это понятие различный смысл. Для нас существенно то, что многие исследователи связывали понятие гармонии с определенным свойством или состоянием целостной системы (произведения искусства, явления природы, состояния человека), рассматривая такое свойство или состояние как идеальное или оптимальное (наилучшее в каком-то отношении). Греческое понятие harmonia означает стройность, соразмерность, уравновешенность элементов в системе. Приведем несколько высказываний о гармонии. «(Неразрывные) сочетания образуют целое и нецелое, сходящееся и расходящееся, созвучие и разногласие, из всего одно и из одного все (образуется)» (Гераклит Темный, V в. до н.э.) [50]. «Расходящееся сходится, и из различного образуется прекраснейшая гармония, и все возникает через борьбу» [51]. «Без соразмерности частей, или, что то же самое, без их взаимной подчиненности, невозможно охватить взглядом целое, потому что иначе глаз принужден беспрестанно перескакивать с места на место» [52]. «Единство целого рождается из подчиненности частей и из этой же подчиненности рождается гармония, которая немыслима вне многообразия» [53]. «Гармония есть результат повторения основной формы произведения в его частях» (А. Тирш) [54].
Если обратиться к словарям, изданным в последние годы, то можно прочитать следующее: «Гармония — согласованное сочетание, соразмерность всех элементов художественного произведения» [55]. «Гармония — соразмерность, согласованность отдельных сторон, предметов и явлений; специфическое единство в многообразии» [56].
Идея гармоничного целого, возникшая в античной философии и искусстве, получила распространение и в науке. Идея гармонии природы в начале ХIX в. нашла свое выражение в теории типов Кювье, который, основываясь на сравнительно-анатомическом и палеонтологическом материале, сформировал представление о типе организации животного как о закономерно построенной целостной системе. К. Бэр обосновал теорию типов на материале сравнительной эмбриологии. Однако в названных теориях абсолютизировалась устойчивость систем, которая неправомерно отождествлялась с неизменностью. А. И. Опарин, характеризуя биохимические процессы и реакции в клетке, пишет, что «специфично для живой материи то, что в протоплазме эти реакции определенным образом организованы во времени, связаны между собой в единую, целостную систему. Они протекают здесь не случайно, а в строго определенной последовательности, в известном гармоническом порядке, который лежит в основе всех жизненных явлений» [57]. В. М. Бехтерев писал: «Мир строится в форме замкнутых систем, представляя собой особые индивидуальности. Каждая индивидуальность может быть различной сложности, но она представляет всегда гармонию частей и обладает своей формой и своей относительной устойчивостью системы» [58].
Введем понятие о гармоничном целом, своего рода идеальном целом по аналогии с идеальным газом, идеальным кристаллом и т. д. Как и последние, гармоничное целое является абстракцией. Из приведенных высказываний следует, что как в искусстве, так и в науке понятие гармонии получило широкое распространение, ибо как искусство, так и наука, являясь различными формами отражения природы, обнаруживают в природе свойство гармоничности. Из тех же высказываний, однако, следует, что в это понятие авторами вкладывается неодинаковый смысл, который содержит, к тому же, большую степень неопределенности. Вместе с тем эти положения фиксируют отдельные свойства гармоничного целого. Может быть поставлен вопрос о том, каким должен быть набор свойств объекта, чтобы он был необходим и достаточен для реализации гармоничного целого. В наших работах [59] была сделана попытка определить состав таких свойств (систему принципов). Анализ произведений искусства, систем природы, а также обширного литературного материала позволил выделить следующие пять принципов гармоничности целого: 1) повторяемость целого в его частях; 2) соподчиненность частей в целом; 3) соразмерность частей и целого; 4) уравновешенность частей в целом; 5) единство целого.
Повторяемость целого в его частях (большое в малом). Этот принцип служит для объединения частей в целое на основе сходства. Части целого обладают различными признаками, среди которых выделяется ведущий — признак целого. Принцип повторяемости означает близость частей композиции по ведущему признаку всего целого. Например, если ведущим признаком целого является определенный цветовой тон, то любые тона всех частей должны содержать в определенной степени этот тон.
Наличие близких значений одного и того же признака создает при восприятии условия для суммации сигналов от различных частей объекта в воспринимающей системе, что способствует возникновению доминирующего перцептивного образа. С другой стороны, близость между частями облегчает перестройку воспринимающих систем при перемене зоны внимания. Но близость частей не означает их тождества; между ними имеются и различия, поэтому при восприятии не возникает быстрой адаптации органов чувств, различия близких элементов создают условия для длительного сохранения внимания на высоком уровне. Вместе с тем разнообразие элементов делает объект восприятия информативно насыщенным, что обеспечивает длительное сохранение активности воспринимающих систем. Однако повторяемость еще не обеспечивает целостности. «Фабула бывает едина не тогда, когда она вращается около одного героя, как думают некоторые; в самом деле, с одним может случиться бесконечное множество событий, даже часть которых не представляет никакого единства» [60]. Множество элементов, объединенных по одному (простому или сложному) признаку, затем может распасться на части. Принцип «большого в малом» необходим, но не достаточен.
Соподчиненность. Принцип соподчиненности служит для объединения частей в целое на основе различия. На основе различия в целом выделяются главное, второстепенное и дополнительное. Принцип соподчиненности означает упорядоченность частей или групп, в которые объединены все элементы целого. Признак, по которому происходит соподчинение, может не совпадать с ведущим признаком, положенным в основу принципа повторяемости. Этот принцип создает в объекте восприятия зоны, неодинаково воздействующие на отражающие системы. Различие между зонами должно легко восприниматься, т. е. оно должно превосходить некоторую пороговую величину. Среди этих зон главная вызовет максимальный эффект в воспринимающей системе и может явиться отправным пунктом в последовательности восприятия. Соподчиненность обеспечивает иерархию зон внимания и предотвращает его колебания.
Соразмерность. Принцип соразмерности служит для согласования частей в целом по их метрическим характеристикам. Каждому признаку соответствует своя метрика, т. е. своя числовая мера. В целом должна существовать общая мера определенного масштаба (размера), с которой должны быть соотнесены все части целого, а величины этих частей и целого должны находиться в определенной закономерной связи. Временные и пространственные величины должны быть согласованы, прежде всего. Например, в Модулоре Корбюзье имеется общая мера признака (длины) и зависимость между числовыми характеристиками этих признаков (золотое сечение). Этот принцип позволяет воспринимающим системам уловить метрическую закономерность связи частей и целого, что обеспечивает активность механизмов антиципации. Количественные закономерности в объекте восприятия улавливаются воспринимающими системами не сразу, но, будучи выявленными, они значительно облегчают процесс восприятия. Таким образом, принцип соразмерности означает СОгласование РАЗмеров МЕР в целом.
Части и целое соразмерны между собой, если они имеют общую меру по какому-либо признаку, а значения этого признака для всех частей и целого могут быть объединены закономерностью определенного вида. В качестве таких закономерностей выделим следующие три типичных числовых последовательности: метрическую прогрессию, арифметическую прогрессию и геометрическую прогрессию. Константой в метрической прогрессии является элемент ряда, в арифметической — разность между соседними элементами, в геометрической — отношения между ними. Таким образом, соразмерность является формой связи между частями и целым.
Уравновешенность. Этот принцип служит для согласования противоположных сторон целостного объекта. Уравновешенность целого — это в частном случае равновесие частей и целого в силовом поле. Для объектов зрительного восприятия — это равновесие относительно пространственных осей. Вертикальная и горизонтальная оси не равноценны; главную роль играет вертикальная ось, что обусловлено гравитацией. Говоря о равновесии объектов восприятия, следует иметь в виду реакции различных подсистем восприятия. Равновесию относительно осей соответствует оптимальное состояние моторики глаза. Уравновешенность обеспечивает устойчивость внимания и баланс системы, воспринимающей цвет.
Принцип единства требует согласования структуры целого и его функции или, в других терминах, согласования цели и средства. В обеспечении этой задачи «участвуют» все перечисленные выше принципы. Принцип повторяемости означает единство по ведущему признаку; соподчиненность — единство, достигаемое объединением всех элементов композиции вокруг главного; соразмерность — это единство, обеспечиваемое общей количественной закономерностью; уравновешенность означает единство, обеспечиваемое согласованием противоположностей. Перечисленные принципы, будучи реализованы в объекте, выступают не изолированно. Они взаимосвязаны друг с другом, дополняют и видоизменяют друг друга. Единство целого можно рассматривать как интегральный его принцип.
Сущность системы принципов гармоничности целого и каждого в отдельности раскрывается более полно, если рассмотреть систему принципов и средств композиции (рис. 1). Дадим краткую характеристику каждого из композиционных средств.
Пластичность. Пластика есть характер границы, который может быть математически описан функциями одной или многих переменных. Например, для линий и поверхностей это могут быть характеристики кривизны. В отличие от пластики пластичность как композиционное средство устанавливает соответствие между свойствами границ: среды и композиции; композиции как целого и ее частей. Когда среда включает человека, необходимо согласование композиции и тела человека; композиции и ее частей с их субъективными эталонами, имеющимися у человека. Таким образом, пластичность есть композиционное средство, устанавливающее соответствие между характеристиками границ. Другие композиционные средства устанавливают соответствие между теми же четырьмя парами компонентов.
Тональность. Тону как характеристике внутренней области можно поставить в соответствие математическое (и физическое) понятие спектра частот. Например, цветовой или звуковой тон, фактура, светлота. Композиционное средство «тональность» устанавливает соответствие между спектрами внутренних областей. Отметим, что тональность, как и пластичность, является характеристикой границы, но пластичность является ее макрохарактеристикой, а тональность — микрохарактеристикой.
Контрастность. Контраст есть разностное отношение двух любых величин, например, разность между большим и малым, светом и тенью и т. п. Контрастность устанавливает соответствие между разностями значений одной и той же характеристики в вышеупомянутых четырех отношениях.
Масштабность. Масштаб есть кратное отношение линейных размеров. Масштабность — это композиционное средство, с помощью которого устанавливается соответствие между кратными отношениями линейных размеров. Контраст и масштаб являются характеристиками различия. Контраст характеризует качественное различие частей композиции, а масштаб — количественное.
Пропорциональность. Пропорция в математике есть равенство отношений. Здесь под пропорцией понимается соотношение однотипных метрических характеристик в различных измерениях, например соотношение длины, высоты, ширины (a:b:c). Пропорциональность есть композиционное средство, с помощью которого устанавливается соответствие между пропорциями.
Ритмичность. Ритм есть закономерное изменение элементов композиции в одном измерении. Ритм может быть описан функцией одной или нескольких переменных и параметров. Ритмичность есть композиционное средство, с помощью которого устанавливается соответствие между параметрами ритмов. Пропорциональность и ритмичность являются характеристиками отношений между элементами композиции. Пропорциональность — характеристика отношений сходства, а ритмичность — отношений порядка.
Симметричность. Симметрия есть степень сходства в расположении. В математике под симметрией понимается инвариант преобразования объекта. Степень симметрии можно характеризовать мерой симметрии. Симметричность — композиционное средство, устанавливающее соответствие между мерами симметрии.
Тектоничность. Тектоника характеризует размещение (распределение) сил и моментов в пространстве композиции. В механике тектоника характеризуется разностями сил, с которыми взаимодействующие части действуют друг на друга в силовом поле (например, в поле тяготения). Тектоничность есть композиционное средство, устанавливающее соответствие между тектоникой среды и композиции, композиции и ее частей, композиции и человека. Симметричность и тектоничность являются характеристиками неизменности композиции, ее инвариантности, причем симметричность характеризует неизменность динамики композиции, а тектоничность — неизменность ее статики.
Структурность. Структура (в данном случае) есть взаиморасположение и взаимосвязь составных частей. В математике структура понимается как совокупность отношений, заданных на некотором множестве. Количественно структура может характеризоваться мерами порядка и связности. Структурность как композиционное средство устанавливает соответствие между мерами порядка и связности в четырех упомянутых выше отношениях.
Функциональность. Функция в математике есть правило, по которому устанавливается однозначное соответствие между двумя множествами. Степень соответствия может характеризоваться мерами соответствия (например, информационными). Функция композиции определяется всегда ее значением в другой системе как в большем целом, что фактически означает соответствие композиции как одного множества и среды как другого множества. Функциональность есть композиционное средство, используемое для согласования мер соответствия.

В системе композиционных средств связь между отдельными средствами обусловливается принципами гармоничности. Это означает, что каждый принцип реализуется совокупностью (группой) средств. Так, например, соразмерность достигается с помощью пропорциональности и ритмичности, а также примыкающих к ней масштабности и симметричности. Согласование (установление соответствия) внутри каждого средства означает применение к набору соответствующих характеристик принципов гармоничности. Тем самым в композиции как процессе возникает обратная связь: принципы реализуются на основе средств, которые в свою очередь используются на основе принципов гармоничности. Такова система принципов, определяющих гармоничное целое. Разумеется, что изложенное здесь — лишь один из возможных подходов к качественному анализу этого сложного понятия.
Как было показано в первой главе, математическое описание сложных объектов является лишь составной частью многоуровневого описания. Но и математическое описание также может быть многоуровневым, использующим различный математический аппарат, наиболее адекватный описываемой реальности. Для описания целого как элемента и как системы, для описания его состава, структуры и интегральных характеристик, для описания статики и динамики целого требуются различные математические абстракции. Любая формальная математическая теория помимо основных постулатов, средств вывода и метрических шкал содержит также и основные идеи и системы понятий. Цель настоящего параграфа состоит в том, чтобы обсудить выбор основных математических идей, понятий и моделей, которые могут быть использованы для описания объектов и процесса восприятия.
Какой математический аппарат адекватен целостным системам? В последние десятилетия разработаны различные подходы к описанию структуры и динамики систем: теория автоматического регулирования, исследование операций, методы многомерного статистического анализа и ряд других. Для описания динамики систем используются аппарат дифференциальных уравнений, теории автоматов, алгоритмы. В качестве общей основы такого описания выступают функциональный анализ и современная алгебра.
Вероятностные и статистические методы используются в тех случаях, когда мы не располагаем полной информацией о системе или когда информация о системе несоизмерима с информационными возможностями отражающей системы, а другие пути сокращения информации не просматриваются. Статистический аппарат совершенно необходим и адекватен для описания нерегулярностей объективного мира. Когда регулярности и нерегулярности разделимы, статистические методы целесообразно использовать только для описания нерегулярного компонента.
Математические модели целостных объектов можно классифицировать как по типам этих объектов, так и по виду применяемого математического аппарата.
Описание целого как элемента. Основными инвариантами целого являются связность и ограниченность. Связное множество топологического пространства — множество, которое нельзя разбить на два непересекающихся непустых открытых множества. В этом множестве можно выделить внутренние и внешние точки. Множество внутренних точек называется областью, множество внешних — границей. Множество точек области и границы образует замкнутую область. Любые две точки области можно соединить линией, целиком состоящей из точек области.
В объектах восприятия связность между элементами может иметь место, как в пространстве объекта, так и в пространстве признаков его элементов. Пространство признаков — это множество возможных значений признаков вместе с метрикой, определенной на этом множестве. Объединение элементов в пространстве признаков может осуществляться не только в случае связности значений признаков (непрерывная шкала значений признака), но и в случае близости значений признака. Если элементы целого находятся в движении, то их признаками могут быть и характеристики движения. Взаимодействие элементов возможно вследствие связности или близости характеристик движения (например, синхронизации). Такую связность можно назвать динамической.
В общем случае могут действовать все перечисленные факторы.
Степень связности области может характеризоваться по-разному. Порядок связности — это натуральное число, равное числу внутренних областей и на единицу меньшее числа контуров. Если введена метрика, то степень связности можно оценить коэффициентом связности.
Множество ограничено, если включает в себя границу. По характеристике ограниченности связные множества делятся на открытые и замкнутые. Замкнутое множество содержит все свои предельные точки. Открытое множество не содержит предельных точек. Множество, включающее в себя лишь часть предельных точек, называется полуоткрытым. Если множество конечно, ограниченно и замкнуто, то оно компактно. Множество называется выпуклым, если любые две его точки могут быть соединены отрезком прямой, все точки которого принадлежат данному множеству.
Понятия связности, ограниченности, компактности, выпуклости являются тем основным набором математических понятий, с помощью которого можно описать основные свойства целого как элемента. Понятия эти могут быть дифференцированы, далее для их оценки можно вводить количественные меры.
Целое как элемент может быть описано и как математическое отношение. Устанавливается множество наблюдаемых признаков целого P(Р1, P2, ..., Pn) в области их значений X(X1, X2, ..., Xn), определяются допустимые комбинации значений. Тогда целое C описывается отношением
C ⊂ X1 × X2 × ... × Xn
С точки зрения логики целое — элемент может рассматриваться как конъюнкция свойств, с одной стороны, и член родовидового отношения — с другой. Объект как конъюнкция есть конъюнкция противоположностей по одной характеристике, и конъюнкция разных характеристик. Как член родовидового отношения объект характеризуется объемом и содержанием.
Целое как система (Алгебраическое описание). Объект рассматривается как конечное множество элементов. Элементами являются как области, так и границы. Как известно, множество задается перечислением элементов или указанием признака принадлежности к данному множеству. Далее будем считать, что множество элементов целого задано перечислением и тем самым определен его состав. Элементы могут иметь некоторое (конечное) число независимых характеристик (признаков) — качественных, порядковых и количественных. Между элементами существуют отношения различного типа. Отношением называется всякое подмножество декартова произведения конечного числа множеств. В алгебре рассматриваются отношения пяти типов: эквивалентности, толерантности, строгого порядка, квазипорядка и нестрогого порядка [61]. Отношения эквивалентности рефлексивны, симметричны и транзитивны. Отношения толерантности рефлексивны и симметричны, отношения строгого порядка транзитивны и антирефлексивны. Отношения квазипорядка рефлексивны и транзитивны. Отношения нестрогого порядка рефлексивны и антисимметричны. В зависимости от числа элементов, входящих в отношение, их называют унарными, бинарными, тернарными и для множества элементов — полиарными. Отношения задаются перечислением подмножеств, для которых верно данное отношение. Бинарные отношения можно задать матрицей или графом. Отношение эквивалентности задает разбиение множества на классы. Отношения порядка устанавливаются: только для некоторых пар элементов (не все элементы сравнимы). В случае нестрогого порядка все элементы сравнимы.
Сравнимость означает наличие общего признака. Рефлексивность означает истинность выражения xAx. Симметричность означает выполнение отношений xAy и yAx, для асимметричных отношений, по крайней мере, одно из них не выполнено. Транзитивность означает, что если xAz и zAy, то xAy.
В связи с этой классификацией отношений на основе их свойств отметим, что эта система отношений не является полной в том смысле, что могут быть определены отношения, не принадлежащие ни к одному из перечисленных классов. Каждое отношение есть некоторое ограничение. Например, объекты, толерантные между собой, должны удовлетворять условиям рефлексивности и симметричности. Но эти ограничения довольно слабы в смысле, что соотносимые объекты могут изменяться в весьма широких пределах без нарушения этих условий.
Для содержательной характеристики близости объектов некоторого множества необходимо вводить качественные и количественные характеристики близости. Эти характеристики могут быть, весьма, различными, например, это может быть расстояние в пространстве признака, наличие общей меры, простота преобразования одного элемента в другой и т. д. Таким образом, алгебраические отношения, наложенные на множество элементов, представляют собой лишь каркас, внутри которого имеется еще достаточно большая свобода для варьирования свойств элементов.
Качественные, сравнительные и измерительные признаки в терминах отношений, существенно, различны [62]. Качественные (классификационные) признаки устанавливаются на основе понятия эквивалентности любым непротиворечивым образом, независимо от того, существуют такие классы в действительности или нет. Сравнительные признаки должны удовлетворять отношениям частичной упорядоченности и фактам природы. Количественные признаки устанавливаются методом счета или методом измерения. Для измерений должна быть указана объективная процедура. Измерение, в отличие от сравнения, требует уже системы отсчета, которая выбирается из реальных условий физического мира. Следует различать отношения на множестве элементов объекта и отношения на множестве словаря элементов (отношения на множестве слов в предложении и отношения на множестве слов в данном языке). Отношения второго типа изучаются семиотикой и в данном контексте не рассматриваются. Однако отметим, что проблема связи между отношениями в языке и отношениями в целом, построенном на основе этого языка, представляет несомненный интерес применительно к описанию целого. В известном смысле, это есть отношение между синтактикой и семантикой, возможным и существующим.
Отношениями связаны все элементы целого. Инвариантные отношения определяют структуру динамического объекта. Структура — функция декомпозиции и признака, по которому устанавливается отношение порядка. Математически структура описывается ориентированным графом, вершины которого соответствуют элементам, а дуги — отношениям. Частным случаем графа является дерево, которое соответствует иерархической структуре. Иерархическая структура характеризуется числом уровней, модулем иерархии (отношение числа элементов на смежных уровнях) и весами ветвей. Для реальных систем эти величины ограничены и в каждом конкретном случае могут быть указаны их оптимальные значения. Веса ветвей различных уровней взаимосвязаны. Динамика процессов в иерархии характеризуется различной полосой пропускания частот различных уровней.
Вопрос о числе компонентов иерархии связан с вопросами числа существенных переменных и числа однородных (и разнородных) компонентов целого. Проблема эта сводится к поиску критерия полноты эмпирических или теоретических характеристик, как по общему их числу, так и по составу. При этом полнота понимается в смысле полноты обеспечения необходимого разнообразия, полноты состава целого, необходимой для выполнения его функций. Многие практические задачи, связанные со структурой и функционированием целостных систем, сводятся к решению задачи определения экстремума (максимума) некоторой (целевой) функции в рамках ограничений, наложенных на ее аргументы. Как известно, общих методов решения этой задачи не существует. В зависимости от имеющейся информации приходится применять разные методы — алгоритмические, поисковые или эвристические. Трудность задачи быстро растет с увеличением числа аргументов целевой функции. Выбор целевой функции, критерия качества также иногда бывает непростой задачей. Целое как система содержит помимо непрерывных и линейных компонентов также дискретные и нелинейные компоненты, что сильно затрудняет математическое описание целого.
Математическое описание динамики целостных систем. В контексте данной работы динамика целостных систем нас будет интересовать в двух аспектах: во-первых, динамической системой является воспринимающий человек; во-вторых, человек может иметь дело с отображением динамической системы.
В настоящее время имеется хорошо разработанный математический аппарат для описания динамики, анализа и синтеза систем весьма широкого класса (теория автоматического управления, теория оптимального управления, теория автоматов, общая теория систем, исследование операций, системотехника и другие). Состояние системы характеризуется набором обобщенных координат, ее поведение — изменением обобщенных координат во времени. Во многих случаях при описании реальных систем возникает необходимость упрощения описания, но упрощения такого, которое сохраняло бы существенную информацию о поведении системы. Два обстоятельства, на которые обратил внимание А. М. Молчанов, помогают произвести упрощение. Он пишет [63]: «...нет надобности рассматривать (по крайней мере, в первом приближении) сразу всю иерархию масштабов и соответствующих им систем. Факт „замирания“, „выключения“ и высших, и низших масштабов времени имеет первостепенное методологическое значение. Он позволяет сводить вопрос к изучению только одной ступеньки, содержащей только два соседних масштаба времени». В другой работе [64] он же отметил, что значимость взаимосвязанных переменных быстро убывает, поэтому часто можно ограничиться небольшим их числом, не совершая при этом грубой ошибки.
Рассмотрим влияние связности на свойства динамической: системы, в частности, на ее устойчивость. Понятие «устойчивость» неоднозначно. Устойчивостью называют способность объекта сохранять неизменными свою целостность, структуру, функцию или пределы изменения существенных переменных при заданном внешнем воздействии. Система может быть одновременно устойчивой в одном и неустойчивой в другом смысле. Например, она может быть целой, но неспособной выполнять свои функции из-за чрезмерно больших колебаний существенных переменных, превышающих область допустимых значений. Часто для обеспечения функциональной устойчивости в изменяющейся среде необходимо изменять параметры или структуру системы (самонастраивающиеся и самоорганизующиеся системы). Математическая теория динамической устойчивости позволяет сделать вывод о том, что неустойчивость системы возрастает с увеличением системы и ее связности. Введение иерархии уменьшает число связей в системе и делает ее более устойчивой.
Проблемы анализа и синтеза целостных систем являются главными задачами общей теории систем и ее разделов (теории автоматов, теории систем автоматического управления). Разработаны методы синтеза искусственных систем некоторых классов и предложены модели эволюции некоторых простейших естественных систем.
Интегральные характеристики целостного объекта. Интегральные характеристики целого определяются его составом и структурой, свойствами частей и отношений. Интегральные характеристики суть функционалы, определенные на множестве элементов объекта. Как уже говорилось, целое есть нечто большее, чем сумма своих частей. Известно, что Аристотель считал это определяющим признаком целого.
Анализ целостных объектов показывает, что они обладают не только аддитивными, но также супераддитивными (данная характеристика целого больше суммы соответствующих характеристик частей) и инфрааддитивными (данная характеристика меньше суммы своих частей) свойствами. Некоторые из таких интегральных характеристик можно определить как линейные (аддитивные) или нелинейные (неаддитивные) функционалы.
Действительный функционал с геометрической точки зрения есть отображение пространства любого числа измерений в одномерное пространство (на числовую прямую). Интегральные характеристики целостного объекта всегда определяются на множестве всех его элементов. В этом смысле интегральные характеристики — всегда глобальные функционалы. Частным случаем функционалов являются линейные функционалы.
Рассмотрим некоторые подходы к количественной оценке разнообразия, регулярности, сложности и некоторых других интегральных характеристик целостных объектов. Для этого необходимо задаться некоторыми характеристиками отражающей системы; выбрать модели объектов и уточнить определение конкретных интегральных характеристик.
Существенными характеристиками отражающей системы будет поле контакта с объектом, объем памяти и набор операций, которые может выполнять система. В качестве моделей было бы полезно использовать такую их последовательность: линейные последовательности букв или цифр, кольцевые последовательности букв или цифр, линейные и кольцевые последовательности векторов, неупорядоченное и частично упорядоченное множество векторов, плоскостные геометрические объекты.
Рассмотрим меры разнообразия. Будем различать разнообразие состава и разнообразие структуры. При любой оценке разнообразия необходимо указать тот предел, при достижении которого объекты становятся неразличимыми. Например, таким пределом может служить инвариант подобия: все подобные объекты считаются неразличимыми.
При анализе состава следует иметь в виду, что в состав могут входить не только непересекающиеся элементы, на которые разбивается целое в результате декомпозиции, но также и объединения элементов, включая и целое. В таком случае уже имеет значение порядок элементов. В этом одна причина непригодности энтропийной оценки. Следует также различать разнообразие состава областей и границ.
Введем меру разнообразия состава ограниченной одномерной последовательности из неметрических элементов. Дан конечный алфавит длины m. Из букв этого алфавита составим последовательность конечной длины. Очевидно, что наименьшим разнообразием будет обладать последовательность, состоящая из одинаковых букв, а наибольшим — последовательность, в которой все буквы различны. Очевидно также, что разнообразие состава увеличивается с увеличением длины последовательности только в том случае, если при этом появляются новые буквы. Поэтому целесообразно выбрать за нулевую точку шкалы разнообразие последовательностей, состоящих из одинаковых букв, а за верхнюю точку шкалы — разнообразие последовательностей, в которых все буквы разные. Примем всю шкалу за единичный отрезок. Тогда вышеуказанным требованиям удовлетворяет следующая мера разнообразия состава: в среднем на одну букву
r = (n - 1) / (N - 1),
где n — число различных букв в последовательности, N — длина последовательности. При (N ≠ 1 и n = 1), r = 0; при (n = N ≠ 1), r = 1; при (n = N = 1), r = 0/0, т. е. неопределенность. Действительно, при одном элементе нельзя говорить о разнообразии состава. Соответственно для всей последовательности разнообразие
R = N × (n -1) / (N - 1).
Из этой формулы следует, что при простом удвоении последовательности разнообразие ее состава практически не увеличивается. Введенные меры разнообразия состава не зависят от порядка и относительных частот букв в последовательности.
До сих пор мы исходили из неявного предположения о том, что все буквы равноценны (имеют равную длительность, занимают одинаковую площадь, имеют одинаковую значимость и т. д.). Но это может быть и не так. Неравноценность букв может быть учтена путем введения весовых коэффициентов. При этом будут видоизменены и формулы для оценки разнообразия состава. Как мы видим, оценка разнообразия состава последовательности заметно отличается от информационных оценок.
В последовательности человек воспринимает не только отдельные буквы, но и группы букв, блоки, причем имеется тенденция ко все большему укрупнению блоков. Укрупняя блоки последовательности, можно построить такую иерархию блоков, верхним уровнем которой будет «блок» всей последовательности. Для оценки разнообразия такой иерархии можно предложить аддитивную оценку вида
ri = 1 / (k - 1) ∑i-1k-1 (ni - 1) / (Ni - 1)
где k — число уровней иерархии, i — порядковый номер уровня.
Для любого k при (ni = 1 и Ni ≠ 1), ri = 0; при ni = Ni ≠ 1, ri = 1. Случай ni = Ni = 1 вырожденный.
Так как иерархия определяет одну из возможных структур последовательности, то величина ri является оценкой разнообразия не только состава, но и этой конкретной структуры.
Если последовательность не ограничена и наблюдается ее конечный отрезок, то нельзя говорить о разнообразии ее состава в вышерассмотренном смысле. Можно оценить алфавит для стационарных последовательностей, безусловные и условные вероятности и энтропии и по ним судить о степени регулярности последовательности. Рассмотрим простой пример последовательности, состоящей из нулей и единиц. Регулярность (закономерность) в такой последовательности может состоять в ее периодичности. Если для таких последовательностей с различной степенью регулярности вычислить ряд значений энтропии H0, H1, H2 и т. д., то для этих последовательностей соответствующие им ряды окажутся различными. Однако вычисление энтропии высоких порядков связано с большими техническими трудностями. Поэтому для оценки нерегулярности в целостном объекте целесообразно применять другие способы (меры асимметрии, аритмии и т. п.).
Если элементами последовательности являются метризованные элементы, например числа, то между ними могут быть установлены отношения порядка. В этом случае меры разнообразия структуры должны учитывать и эти отношения, но могут быть введены специальные меры упорядоченности. На множестве элементов последовательности могут быть заданы системы операций, с помощью которых получаются новые элементы. Это еще более затрудняет оценку разнообразия структуры.
Если элементы последовательности (или любого целостного объекта) многомерны, то возможны два подхода к оценке разнообразия состава: сведение многомерной модели к одномерной путем увеличения алфавита или сведение n-мерной модели к системе n одномерных моделей.
В каком отношении меры разнообразия находятся к другим интегральным характеристикам? Меры упорядоченности характеризуют одну из структур — структуру порядка. Меры однородности характеризуют главным образом состав, его распределение в пространстве. Меры регулярности характеризуют возможность обратимого сокращения разнообразия.
В работах, посвященных восприятию, все чаще фигурирует понятие «отображение». Его применение представляется весьма целесообразным и продуктивным, если имеется в виду математическое содержание этого понятия.
Восприятие целостного объекта можно рассматривать как отображение объективного множества — объекта в субъективное множество — образ. Множество-объект является подмножеством перцептивного пространства, множество-образ — подмножеством субъективного пространства. Такая интерпретация восприятия целостного объекта позволяет описать его в терминах отображения множества.
Понятие «отображение» в математике является синонимом понятий «преобразование», «функция», «оператор». Во всех случаях для определения отображения нужно задать: два произвольных непустых множества (X и Y), правило, закон соответствия элементов этих множеств Y=f(X), подмножество Df — область определения функции f, подмножество Rf — область значений функции f (рис. 2) [65]. Для каждого подмножества A из Df функция f ставит в соответствие некоторое подмножество В из Rf. Подмножество A называется прообразом, подмножество B — образом A.
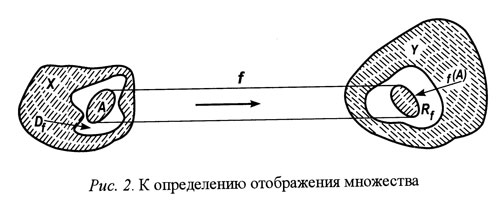
Конкретный вид отображения определяется многими факторами, главными из которых являются: мощность и другие характеристики множеств, между которыми устанавливается соответствие; вид функции, область определения функции. Соответствие между элементами одного и того же множества называется отображением в себя. Частным случаем отображения является взаимнооднозначное соответствие (изоморфизм). Многие преобразования образуют группу. Преобразования могут быть непрерывными и дискретными, параллельными и последовательными. Преобразователи могут иметь память и не иметь ее. Преобразования без памяти каждому подмножеству A ставят в соответствие всегда одно и то же подмножество B. Результат преобразования с памятью зависит, кроме исходного множества, также от состояния преобразователя в момент функционирования.
Восприятие целостного объекта (отображение I) и целенаправленное действие, поведение, продуктивная деятельность (отображение II) являются частными, но весьма сложными видами отображений. Хотя при их описании математические понятия весьма полезны, однако, для полного их математического описания современный аппарат недостаточен. Одно из преимуществ применения математических понятий состоит в том, что с их помощью в таких разных психических процессах, как отражение и поведение, восприятие и действие, познание и творчество, отражение и преобразование, можно обнаружить общее, описать их на одном языке.