

Говорят, что между двумя противоположными мнениями находится истина. Ни в коем случае! Между ними лежит проблема.
Вольфганг Гете
 егко прослеживается закономерность, о которой говорил еще в 60-е годы известный советский кибернетик М. М. Бонгард — реальная эффективность усилий ученого зависит не только от его способностей получать содержательные результаты, но и от того, к какой науке, к какой области человеческой практики он относит свои результаты. Общество более охотно «подает» на определенный ярлык: в свое время фаворитом выступала кибернетика, затем им стала бионика, в наше время — искусственный интеллект и информатика.
егко прослеживается закономерность, о которой говорил еще в 60-е годы известный советский кибернетик М. М. Бонгард — реальная эффективность усилий ученого зависит не только от его способностей получать содержательные результаты, но и от того, к какой науке, к какой области человеческой практики он относит свои результаты. Общество более охотно «подает» на определенный ярлык: в свое время фаворитом выступала кибернетика, затем им стала бионика, в наше время — искусственный интеллект и информатика.
К чему приклеена модная этикетка «искусственный интеллект»? Заметим, что содержание понятия, выраженного этой комбинацией слов, менялось со временем: поначалу в фокусе внимания находились проблемы эвристики, затем — алгоритмы распознавания, далее — способы организации памяти (фреймы, структуры знаний). Так, Н. Н. Моисеев [124] отмечает, что в специальной литературе искусственным интеллектом принято называть новую технологию работы с информацией, включающей в себя способы обращения с базами данных, процедуры ее переработки и вспомогательные средства, помогающие пользователю контактировать с компьютером.
Как мы считаем, в последнее время центральное место занимает вопрос о том, как человек решает интеллектуальные задачи.
Под названием «искусственный интеллект» теперь объединяют ряд проблем, одна из которых — разработка языка картинок (икон). Иконический язык как формализованный набор команд в картинках для компьютеров способен в значительной мере упростить трудный для большинства людей язык программирования, существенно облегчив взаимодействие пользователя с вычислительной машиной.
Другая проблема — создание алгоритмов, которые обеспечат компьютерам способность обучаться, или, иначе говоря, изменяться под влиянием собственного опыта. Последняя задача непосредственно связана со структурированием знаний, в частности знаний для экспертных систем. Здесь следует замерить, что название «экспертные» эти системы пока оправдывают в очень слабой степени. Сейчас они представляют собой лишь склад знаний, которыми обладают различные эксперты, и только в этом смысле могут принести пользу при определенных обстоятельствах. Ведь эксперт оценивается не только по его эрудиции, но и по тому, как он справляется с ситуацией, где события получают новый оборот, не встречавшийся в учебниках. Как известно, действуя в новой ситуации, эксперт использует кроме знаний «что делать», знания «как делать», т. е. применяет разнообразные стратегии решения профессиональных задач, а не просто активизирует даже хорошо организованную пассивную информацию [151].
Ядром современных экспертных систем служат фреймы. Представление знания фреймами позволяет более адекватно соотнести представление знаний в памяти систем искусственного интеллекта с мышлением человека посредством выделения и заполнения фрейма — крупной, структурированной единицы знаний, основанной на фактах или процедурах. Здесь следует пояснить, что понимается под фактуальным и процедурным знанием [79]. Фактуальные (декларативные) знания — база данных — информация о конкретных фактах, собираемая посредством диалога с экспертом. Именно он, основываясь на опыте, указывает, какие факты считать истинными. Важнейшая часть базы данных — сценарий, описывающий внешнюю обстановку, с которой взаимодействует эксперт. (Это знания, объявленные, оречевленные, явные, «А это А».) Процедурные знания — множество правил вывода (продукций) для базы знаний. Здесь подразумевается, что декларативные знания могут преобразовываться в системе по неким правилам, например, по правилам вида «если — то». Правила включают информацию о методах сужения области поиска.
Помимо декларативных и процедурных знаний, современные системы включают управляющие знания — набор стратегий оптимизации решения, которые опираются на метазнания системы о своей работе, своей структуре, своей памяти и схеме рассуждений. Поскольку они определяют уровень компетентности системы, постольку они содержат сведения, касающиеся способов использования знаний и их свойств.
Обратим внимание на то, что совершенствование и развитие современных экспертных систем привело к возникновению структур, в чем-то аналогичных самосознанию (метазнания). Как известно, у человека именно эта система управляет переводом неосознаваемых знаний в осознанные.
Возвращаясь к организации памяти искусственного интеллекта, отметим, что отдельные фреймы взаимосвязаны и образуют единую систему, в которой органически объединены декларативные и процедурные знания. Единство системы реализуется с помощью дополнительной информации, содержащейся в каждом фрейме. Она включает сведения о способе обращения с данным фреймом, о следующем действии, о действии, которое нужно выполнить, если текущие предположения не оправдались. Таким образом, фрейм включает способы переадресации к другому фрейму, а иногда переадресация осуществляется по аналогии [79].
Чрезвычайно интересной в плане данной книги представляется используемая во фреймах операция по умолчанию. Она включается, если не хватает конкретной информации для использования данного фрейма. Тогда вводится предположение, что недостающая информация — обычная, т. е. не отличается от нормы. Такой прием позволяет снять неопределенность — понять смысл ситуации при неполноте информации, однако он создает предпосылки к возникновению ошибки. Вывод по умолчанию выполняет весьма важную функцию при распознавании. Например, если видна лишь часть образа, то, заменив другие части значениями по умолчанию, можно обрисовать полный образ. Точно так же, используя значения по умолчанию, можно восстановить смысл контекста, из которого выхвачены отдельные предложения [151].
Еще одна характерная особенность фрейма связана с наследованием атрибутов, что позволяет избегать дублирования информации и устранять противоречивые знания. При этом указывается и характер наследования: абстрактное или конкретное. Важно, что в качестве идентификатора фрейма используется имя, единственное для данной системы. И характер наследования и уникальность имени соотносят фреймы с правосторонними механизмами. Перечисляя свойства фреймов и формализованные операции с ними, нельзя забывать, что формирование самих фреймов осуществляется не закономерно, логически, а на базе интуиции и опыта.
Роль логических структур в системах искусственного интеллекта непрерывно меняется. Так, в современных экспертных системах все знания описаны в форме систем продукций — множества правил — как наиболее простого способа представления знаний в форме «если — то». Здесь трансляция на язык логических выражений сопоставляется с пониманием, под которым подразумевается автоматическое преобразование предложений, написанных на естественном языке, в язык формальных систем типа логики предикатов. Для представления внутренне непротиворечивой совокупности знаний используют систему логики предикатов первого порядка и вывод заключений через силлогизмы.
Логика предикатов позволяет выяснить, имеются ли противоречия между новыми знаниями и уже существующими в системе. Подобные логические модели, работающие по правилам «если — то», обладают важным достоинством — простотой. Их простота есть следствие двухцветного, а не многокрасочного представления всех описаний, но она эффективна в однородных по своим свойствам задачах, а эффективность решения более сложных проблем, состоящих из нескольких разнородных задач, резко падает. Поэтому не удивительно, что растет неудовлетворенность тем, что, обладая формальной логикой, компьютеры не владеют интуицией, широко используемой человеком для творческого решения задач, не допускающих из-за своей сложности последовательного анализа. Отсюда всевозрастающий интерес к углубленному изучению психологии интуиции и формализации ее механизмов.
В современных системах, особенно экспертных, процесс обработки поступающих данных опирается на сохраняемые в памяти обобщенные знания о всей проблемной области. Это позволяет системе стать более гибкой (интеллектуальной): она может выбирать любую программу из своей памяти или из нескольких программ создать новую. Для того чтобы осмысленно использовать знания о проблемной области, они организованы в иерархические структуры, которые связываются в единое целое с помощью разнообразных отношений между информативными элементами. Причем система остается открытой, т. е. способной к накоплению новых знаний. Здесь нам важно подчеркнуть, что для создания и эксплуатации подобных искусственных иерархических структур нужна система ценностных ориентиров, подобная той, что цементирует и ориентирует модели мира у человека. Так, в работе Н. Н. Моисеева [124] представлена одна из первых систем искусственного интеллекта, где самым важным элементом является блок формирования целей на основе заданных ценностей. Использование системы критериев и ценностей делает систему способной осуществлять не только точные, но и приближенные правдоподобные рассуждения, свойственные человеку.
Некие аналогии с особенностями правосторонней организации и присущими ей способами использования памяти можно усмотреть в системе Hearsay — IL [151], разработанной в американском университете Карнеги-Меллон. Особый интерес в ней представляет модель так называемой доски объявлений, где каждой из проблем, которые в совокупности составляют единое целое, соответствует множество знаний. Причем через общую рабочую область памяти (доску объявлений) информация организуется так, что все знания используются в системе как единое целое. Такая модель обеспечивает согласованную работу разных уровней иерархии представления проблемы. На доске объявлений все гипотезы иерархически упорядочены, на самом верхнем уровне находятся заключения, на самом нижнем — факты, на промежуточных — промежуточные гипотезы (предложение → часть предложения → слово → слог → фонема).
Чрезвычайно актуальной оказалась и проблема формализации представлений здравого смысла. (Здравый смысл — это правила вывода, используемые обыденным сознанием с учетом системы барьеров, стереотипов и элементов интуиции.) Теперь уже нет сомнений, что проблема значительно сложнее, чем можно было первоначально предположить. Это особенно отчетливо обнаружилось после того, как исчезли высказанные Минским надежды разрешить ее путем каталогизирования нескольких сотен тысяч фактов. Однако в процессе решения проблем здравого смысла выяснилось, что наиболее эффективное средство упростить задачу — использовать специальные языки, включающие непроцедурные представления (семантику декларативного типа), в то время как традиционный компьютер оперирует с языками описания процедурного типа (операционной семантикой).
Проблемы метазнания высветили значимость изучения взаимосвязи сознания и подсознательных процессов. Некоторые специалисты уже не сомневаются в актуальности для искусственного интеллекта алгоритмизации не только подсознательных умственных механизмов, но и сенсомоторного интеллекта, а также человеческих эмоций. Как уже упоминалось, структура экспертной системы, кроме блока представления знаний (базы данных) и механизмов логического вывода, осуществляемых на основе этой базы, включает блок, выдающий пользователю различные комментарии к последующему логическому выводу, поясняющие его мотивы. Необходимость в подобных комментариях поясняет Фейгенбаум [243, с. 100]: «По опыту известно, что большая часть знаний в конкретной предметной области остается личной собственностью эксперта. И это происходит не потому, что он не хочет разглашать своих секретов, а потому, что он не в состоянии сделать это — ведь эксперт знает гораздо больше, чем сам осознает». Иначе говоря, необходимо научиться извлекать знания, которыми подсознательно владеет специалист, и для этого в экспертные системы вводится модуль советов и объяснений. В подсознательный багаж специалиста включены такие знания, как «способы сосредоточения», «способы удаления бесполезных идей», «способы использования нечеткой информации» и т. д.
Что и как осознает человек, в чем он хочет и может себе сознаться, а что остается за барьером и не осознается полностью, зависит от его системы психологической защиты и мыслительных стереотипов. Эти моменты уже подробно рассматривались. Здесь целесообразно сделать отступление и обсудить, что тормозит развитие искусственного интеллекта. Создается впечатление, что одной из причин может служить воздействие на его разработчиков психологических барьеров. У них подсознательно могут возникать опасения, что такие черты, как объективность, индивидуальность, идиосинкразия (непереносимость каких-либо задач и подходов к решению), считавшиеся до настоящего времени исключительно человеческим достоянием, — все они, делающие человеческую жизнь столь особенной, а человека как личность — столь интересным во взаимодействии, станут присущими и компьютеру. Что тогда останется человеку? Эта мысль ведь не всех должна вдохновлять?
Если бросить общий взгляд на новые направления в исследованиях искуственного интеллекта, становится понятным, что они не составляют случайный набор, а могут быть представлены как отдельные стороны задач и проблем, отражающих вторжение присущих человеку правополушарных механизмов и правой модели мира в целом в общие схемы искусственного интеллекта. Эта картина свидетельствует о растущем понимании необходимости учета в них того, что сопоставимо с закономерностями взаимодействия правой и левой моделей в ходе решения сложной задачи.
Действительно, применение языка картин в искусственном интеллекте определяется эффективностью правополушарного языка в решении любой задачи. Фрейм также реализует специфическую организацию операций правого полушария, поскольку все свойства фреймов порождены особенностями правосторонних систем памяти и интеллектуальных операций. К ним относятся и укрупненные блоки ситуативной, а не категориально объединенной информации, и связь с биографическими особенностями накопления опыта — декларативным знанием, и оперирование через непрерывные трансформации, и переадресация не по перечню свойств, а по имени и аналогии, и оперирование по умолчанию — распространение старых знаний на новые области, и наследование свойств как следствие непрерывных деформаций. К группе феноменов межполушарного взаимодействия можно отнести понимание как следствие перевода из исходного языка на логический, приемы, способствующие осознанию подсознательно применяемых знаний, метод доски объявлений как объединение структур памяти слева — классификации деревьев и систем памяти справа — иерархии значений.
В первой главе описаны два языка мозга, соответствующие им две модели мира и механизм интуиции, функционирующий на основе специфики взаимодействия полушарий. В этом контексте интуиция предстает как циклический, многоэтапный процесс поочередного доминирования каждого полушария со всеми особенностями его восприятия, памяти и мышления, а также осознанных и подсознательных процессов. Таким образом, общее направление эволюции проблемы искусственного интеллекта вкладывается в развиваемые в этой книге представления о взаимодействии двух моделей мира.
В данной главе усилия сконцентрированы на метриках правой и левой моделей мира — способах описания объектов и их отношений в каждой модели при разных уровнях накопленного опыта. В качестве примеров решения различных задач в метрике обоих полушарий рассмотрены классификация и распознавание. Показано, как формируются структуры знаний в процессе классификации зрительных фигур по сложности и регулярности и как можно представить переход от одной структуры к другой. При решении конкретных задач распознавания структуры знаний (деревья) предполагаются уже сформированными, управляя процессом выдвижения гипотез о классе, они предопределяют сокращение перебора. Алгоритм распознавания включает непременное взаимодействие признаков, выявляемых левым и правым полушариями, и удачная их композиция вносит свой вклад в сокращение перебора.
Прежде чем переходить к конкретным примерам использования описанных выше идей, обратимся к изложению наших представлений о метриках левой и правой моделей мира.
Основываясь на своем представлении специфики процессов в левом и правом полушариях [55, 56, 58, 253], мы предполагаем, что у младенца оба полушария головного мозга функционируют по правополушарным принципам преобразования информации. Постепенно в процессе разделения функций (латерализации) левое полушарие берет на себя функции дискриминации, анализа, а также логического объединения признаков, выделенных из внешней среды правым полушарием. Развитие у человека способности расчленять среду на все большее число элементов вызывает рост числа степеней свободы для объединения элементов по разным основаниям, что, в свою очередь, позволяет все более гибко приспосабливаться к изменяющимся условиям среды.
По мере углубления латерализации, ребенок переходит от врожденно-одномоментного целостного правостороннего восприятия к последовательному преобразованию информации левым полушарием. Совершенствование переработки информации левым полушарием ведет к вторично обобщенному ее преобразованию. Например, при тренировке навыка чтения развивается способность воспринимать не только отдельные буквы, но и группы букв, целые слова и предложения, т. е. все более укрупненные блоки.
Накопленные экспериментальные данные подтверждают предположение о том, что локальное восприятие переходит в обобщенное, по мере обучения. Показано, что в процессе индивидуального развития сокращается число фиксаций глаз при восприятии объекта за счет «неинформативных», что ускоряет опознание. Так, в работах Брунера [34] вскрыта роль развития действий при формировании одномоментности восприятия. Он показал, что сложность организации поля восприятия у ребенка ниже, чем у взрослого. Дети обращают внимание в основном на общие особенности окружения. Упражняясь в узнавании и идентификации, они постепенно начинают реагировать и на мелкие детали. Между ранним детством и восемью годами количество различаемых деталей увеличивается, но лишь к десяти годам детали объединяются в целостную картину. Однако у взрослого можно уловить переход от элементов к целому в сокращенном виде. Иллюстрацией перехода от дискретной картины к вторичной, обобщенной в образе, могут служить эксперименты Мандлеров [264]. Испытуемые должны были без контроля зрения пройти довольно сложный лабиринт. Продолжая проходить лабиринт уже после того, как они овладели этим действием, они начали отмечать изменения в своем решении задачи: вместо программы последовательных движений у них появился зрительный образ пути в лабиринте, который позволял видеть перспективу лабиринта вне связи с движениями.
Анализ по локальным признакам. На не слишком ранних этапах обучения, когда уже сформировался навык выделения локальных признаков, зрительное восприятие формы можно в первом приближении рассматривать как одноканальный процесс, направляемый свойствами объекта и включающий, прежде всего, обследование внешнего контура. В этом процессе формируется перцептивный код, допускающий однозначное восстановление объекта. Такое представление характера восприятия близко к позиции ассоциативной психологии, так как здесь объект выступает как сумма его отдельных свойств.
На более поздних этапах обучения восприятие направляется не только свойствами реального объекта, но и информацией, накопленной в памяти, где организуются системы, позволяющие строить гипотезы. Изменяется система действий при анализе объекта: теперь его надо не описывать, а только отличать внутри класса — достаточно характеризовать обобщенными признаками. С их помощью объект восстанавливается только как представитель класса, а его индивидуальные свойства, позволяющие отличить его от других элементов класса, в признаках не отражены. Процесс восприятия по обобщенным признакам уже несколько ближе к особенности целостного восприятия, которую подчеркивает гештальтпсихология.
Многолетние исследования привели нас к убеждению, что на непрерывном пути усовершенствования зрительного восприятия и опознания можно выделить несколько этапов и с каждым соотнести группу признаков [57, 58, 249]. Первый этап характеризуется выраженностью двигательных компонент, развертывающихся при сканировании контура, который представляет собой наиболее информативную часть зрительного объекта. Как известно, способность к выделению контура совершенствуется у детей параллельно с организацией их внимания. На некоторой фазе своего развития ребенок уже может удерживать внимание на одном предмете достаточно времени, чтобы оглядеть весь его контур. С этого момента он способен узнавать фигуру точнее, объединяя с помощью следящих движений глаз информацию об отдельных участках ее контура в единый код, который формируется на основе врожденных способностей зрительной системы к восприятию перепадов освещенности и кривизны. Выделение контура — такое преобразование исходного множества точек различной яркости многотонового объекта, при котором формируется множество элементов меньшей размерности.
Информация о контуре может использоваться на следующем этапе обработки — для выделения локальных признаков. С этой целью контур разбивается на участки с помощью операции сравнения значения кривизны в каждой точке с некоторым порогом. Число точек разбиения определяется решаемой задачей: не только свойствами самого контура, но и переменной чувствительностью воспринимающих элементов. В нервной системе найдены нейроны и их ансамбли, способные реализовать операции, необходимые для разбиения контура на интервалы.
Контур разбивается на тем большее число участков, чем больше на нем точек, в которых кривизна превосходит порог, т. е. чем он сложнее в рамках одной и той же зрительной задачи. Поэтому более простые фигуры, имеющие меньше элементов, на которых задерживается внимание, кодируются быстрее, чем сложные. Разбиение контура при кодировании по этому правилу отличается от формальных разбиений, когда число интервалов заранее задано (например, размером элемента решетки) и не связано со сложностью изображения. Формальное разбиение, принятое в технических системах, приводит к тому, что простые объекты кодируются избыточно долго, а сложные — недостаточно точно.
В процессе анализа контура формируется первичный код, на основании которого может происходить опознание объекта. Код включает признаки, характеризующие кривизну линии контура на одном интервале или ее длину. Границами интервалов служат точки, где функция кривизны терпит разрыв первого рода — скачок, где значение функции равно некоторой постоянной величине — порогу, где кривизна равна нулю. По этому правилу контур разбивается на конечное число интервалов трех типов: отрезок прямой, дуга окружности малого радиуса (соответствующая на контуре углу, поэтому мы будем для простоты называть такие участки углами), и участок с конечной кривизной. При разбиении контура на интервалы вновь, как и при его выделении, происходит уменьшение размерности — вместо бесконечного числа точек контура для характеристики объекта используется конечное число локальных признаков.
Первый, низший, уровень системы признаков составляют гак называемые локальные (первичные) признаки объекта, характеризующие свойства отдельных участков его контура. Перечислим некоторые свойства линии на интервале, сопоставляемые с локальными признаками: прямая или кривая, положительный или отрицательный знак функции кривизны — выпуклость или вогнутость, следующий признак позволяет отличить участки с изломом от участков с плавной кривой или прямолинейных, другой — участки с постоянной или с переменной кривизной, еще два признака отражают количественное изменение значения кривизны в пределах одного интервала контура и линейные размеры интервала. Информация о свойствах всего контура поступает в память, в виде последовательности первичных признаков — первичного кода — который отражает свойства интервалов контура в том порядке, как они получены при непрерывном сканировании объекта. При формировании первичного кода в каждый следующий момент один интервал контура анализируется одновременно по группе локальных признаков. Первичный код приобретает вид таблицы, каждый столбец которой — последовательность различных признаков одного интервала контура, а строка — последовательность, характеризующая все интервалы по одному признаку.
Обход контура при кодировании может начинаться из произвольной точки, поэтому первичный код всегда инвариантен относительно циклической перестановки столбцов. Сравнение первичных кодов объектов можно соотнести с наложением их контуров друг на друга и поворотом до полного совмещения одинаковых участков. Инвариантность первичного кода относительно других преобразований может меняться в зависимости от различных наборов локальных признаков. Например, если не учитывается длина интервалов, код инвариантен относительно подобных преобразований. Количество признаков и число уровней квантования отдельных признаков определяются требуемой точностью. С локальными признаками можно соотнести топологические, которые использовались нами при распознавании рукописных букв, где одним из ведущих признаков выступал порядок узла.
Обобщенные признаки. В результате преобразования первичной информации, накопленной о разных объектах в памяти, в ней формируется более обобщенное представление о них определяющее дальнейшие изменения способа осмотра изображения, при этом сокращается количество глазодвигательных операций.
Изменение процессов восприятия и памяти при обучении; можно представить следующим образом. Локальные признаки, организованные в первичный код при сканировании объекта поступают в память. В результате многоступенчатого преобразования первичного кода в структурах памяти из него формируются вторичные признаки. Преобразование может включать мыслительные операции анализа информации, выделения новых элементов и объединения их по новым правилам. (Мыслительные операции — это внутренние действия, на основе которых восприятие, первоначально носившее характер внешнего действия, выполнявшегося в значительной мере во внешнем поле, частично переносится во внутренний план. Эти действия совершаются не с реальными предметами и объектами, а с их кодами, символами, знаками.)
Один из видов преобразования — обобщение. Оно может осуществляться посредством ряда логических операций, включающих в себя продольную и поперечную фильтрации, компрессию и суммацию. С помощью этих операций из матрицы первичного кода выделяются либо строка (последовательность градаций одного первичного признака), либо столбцы, имеющие заданное значение одного из признаков. При компрессии группы последовательных одинаковых элементов всегда заменяются одним элементом, а при суммации перечисление признаков заменяется числом.
В отличие от первичного кода, который формируется в процессе последовательного сканирования контура, обобщенные (вторичные) признаки формируются в памяти в результате анализа таблицы первичного кода. Для того чтобы осуществить подобный анализ, необходимо удерживать первичный код. Таким образом, вторичные признаки не могут быть сформированы вне памяти.
Вторичные признаки — это такие характеристики контура, как число углов (ранг), число вогнутостей, изрезанность (число участков с изломом), изогнутость (суммарный угол поворота сканирующего вектора при обходе всего контура), т. е. это функционалы, зависящие от значений всех углов фигуры, но не зависящие от порядка их следования.
Вторичный код объекта в отличие от упорядоченной таблицы первичного кода — неупорядоченная строка. Он инвариантен относительно движения объекта на плоскости и отражает отношение не между отдельными участками, а между их совокупностями. Формирование вторичных кодов изменяет характер обследования объектов — изменяет стратегию осмотра при последующем их восприятии.
Если первичный код позволяет восстановить контур определенного конкретного объекта с его индивидуальными особенностями, то по вторичному коду можно восстановить только обобщенный портрет класса изображений. Поскольку анализ класса объектов произведен в памяти, не вся обработка воспринимаемого изображения происходит во внешнем поле, часть операций выполняется во внутреннем поле (при участии структур памяти) и в дальнейшем при узнавании используется в готовом виде, что повышает скорость узнавания. Вторичные признаки могут использоваться в тех задачах, где важно повысить скорость опознания, а снижение точности не влияет на результат.
Новая стратегия осмотра определяется не только свойствами контура, но и системой гипотез, сформированных на основе накопленной в памяти информации. Человек как бы по-новому смотрит на тот же самый объект, обследуя его последовательно, но не по линии контура, а скачкообразно по информативным точкам. В движениях глаз, ранее жестко привязанных к контуру, появляется больше свободы. При этом расширяется оперативное поле восприятия, увеличивается часть объекта, обрабатываемая одновременно: вместо одного интервала анализу подвергаются несколько участков в окрестностях точки фиксации.
Третичные и позиционные признаки. Запоминание вторичных кодов и дальнейшее их преобразование в памяти позволяют человеку вновь изменить характер осмотра и анализа воспринимаемого объекта, соответственно формируются и новые группы еще более обобщенных признаков — третичные и позиционные. Третичные признаки характеризуют не сам контур объекта, а его соотношения с контуром другого, вспомогательного объекта, например, с его оболочкой. Поскольку вспомогательные объекты могут быть построены мысленно, постольку при формировании этих признаков еще большая часть операций (по сравнению с вычислением вторичных признаков) может производиться во внутреннем поле и при узнавании использоваться в готовом виде. Поэтому восприятие на основе этих признаков происходит с еще большей скоростью и эффективно, когда некоторая дополнительная потеря точности при узнавании объекта несущественна.
Третичные признаки — это функционалы, зависящие от проекций объекта на фиксированные направления, от его площади или от того и другого. К третичным признакам могут быть отнесены удлиненность, компактность, площадь, к позиционным — ориентация. Компактность отражает степень заполнения фигурой ее выпуклой оболочки и вычисляется как отношение площадей фигуры и оболочки. Удлиненность измеряется отношением длин наибольшей и наименьшей осей оболочки. При вычислении ориентации человек соотносит объект с мысленно построенной системой координат. В процессе решения зрительной задачи он переносит внимание с фигуры на фигуру и соответственно переносит построенную координатную систему. Ориентация определяется либо для одного объекта, либо для каждого относительно остальных. Для отдельного объекта ориентацией могут служить, например, наклон главной оси фигуры или ее оболочки.
Третичные признаки (кроме ориентации) характеризуют объект через свойства его оболочки и инвариантны относительно движения объекта на плоскости. С помощью грубой оценки можно показать, что вычисление более обобщенного признака требует большего числа операций, чем локального. Обобщенный признак содержит локальные в снятом виде, и именно это в конечном счете ускоряет узнавание при использовании обобщенных признаков.
Дальнейшее движение по иерархии левосторонних признаков приводит к транспозиционным признакам сходства. Они обозначаются такими словами, как «похож», «напоминает» и т. д. Вычисление признаков сходства в еще большей мере включает операции в памяти. При выявлении таких признаков отображения объектов соотносятся в мысленном поле с многомерной системой координат, где каждая ось — признак, по которому сравниваются объекты. Результаты операций сравнения — положения объектов относительно всех осей выбранного пространства признаков — и есть транспозиционные признаки сходства. Они хранятся в памяти как сведения о степени совпадения объектов. Это информация не о свойствах самих объектов, а только об отношениях этих свойств.
Сходство может отражать субъективные представления людей о близости объектов по форме. На рис. 19 приведено дерево восьмиугольников — тестовых фигур. По одной вертикали расположены фигуры с одинаковыми градациями четырех признаков: ранг (число углов), ориентация, площадь, изрезанность; эти фигуры неразличимы в пространстве перечисленных признаков. Нетрудно видеть, что фигуры одного столбца более похожи, чем фигуры из разных столбцов.
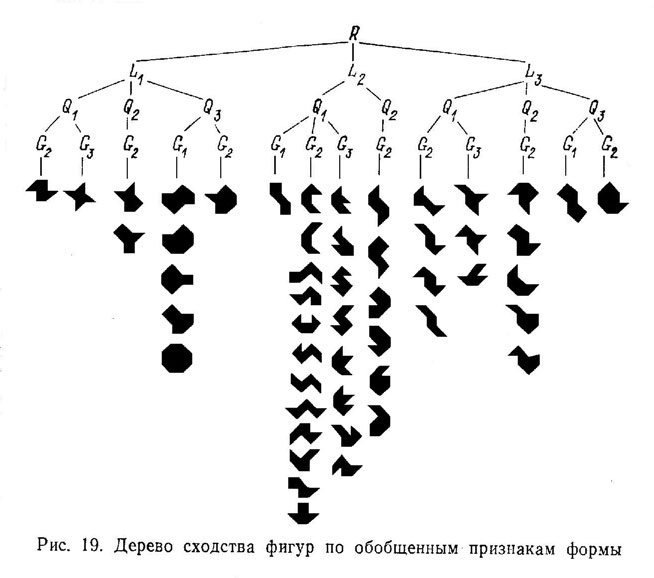
По мере обучения человек формирует, запоминает и хранит для каждого объекта коды разного уровня обобщенности, т. е. в памяти информация об объекте может быть представлена многократно. Эффективность решения конкретной задачи связана с возможностью выбрать код нужного уровня обобщенности из одновременно представленного в памяти набора кодов одного и того же объекта. При использовании различных признаков меняется — расширяется — объем оперативного поля восприятия: только часть объекта, весь объект, объект и части фона, несколько объектов, что позволяет установить взаимные отношения нескольких объектов.
Владея всеми уровнями признаков одновременно, человек может переходить от одних к другим, гибко менять стратегию решения в зависимости от характера задачи. Для того чтобы выделить иную информацию из того же изображения, он перестраивает свое зрительное поле. Изменение фокусировки глаз как бы меняет пространственное положение наблюдателя. Это позволяет ему видеть воспринимаемое изображение по-разному: либо более подробно во всех деталях — и тогда он как бы приближается к объекту, либо более обобщенно — и тогда он как бы удаляется от него.
При формировании вторичных кодов из первичных происходит абстрагирование от некоторых индивидуальных свойств данного объекта: от порядка следования участков контура с одинаковым значением первичного признака (при операции суммации), от числа идущих подряд однотипных по данному признаку интервалов (при компрессии). Объект, восстановленный по вторичному коду, совпадает с множеством других, отличающихся от данного опущенными при абстрагировании качествами. Иными словами, вторичный код — характеристика общности нескольких объектов. Представление об объекте, составленное на основе признаков более высоких порядков, еще меньше напоминает данный единичный объект, поскольку характеризует не его самого, а общность более широкого класса, куда каждый объект входит как элемент.
Чем выше уровень, тем меньше признаки связаны только с конкретной формой объекта, тем более обобщенные черты изображения записываются в памяти, преобразуются в ней, сравниваются в процессе узнавания. А так как объем оперативной памяти ограничен, то при повышении степени обобщенности оперативных единиц хранения, используемых в качестве признаков, растет информативный объем оперативного поля, что повышает интеллектуальные возможности человека. Одновременно с повышением степени обобщенности признаков растет их помехоустойчивость.
Чем выше порядок признака, тем больше операций категоризации он содержит в себе в скрытом виде, тем большая часть операций производится мысленно, в памяти. Движение от низшего уровня ко все более высоким соответствует постепенному переходу при узнавании от действий только с объектом через сочетание действий с объектом и информацией, хранящейся в памяти, к действиям главным образом с информацией в памяти. Способность оперировать обобщенными символами создает огромное преимущество в сравнении с ситуациями, когда можно реагировать только на перцептивную сторону объекта. Оно состоит в том, что в первом случае в момент узнавания практически нет необходимости выполнять все логические операции — они уже вычислены в процессе обучения и в снятом виде хранятся в памяти.
Если человек владеет признаками всех уровней и восприятие происходит в оптимальных условиях, алгоритм узнавания может быть представлен следующим образом. Сложное изображение в поле зрения классифицируется с помощью наиболее обобщенных признаков — транспозиционных признаков сходства. Если узнавания с такой точностью недостаточно, выделенный класс снова разделяется на подклассы посредством менее обобщенных признаков — позиционных и третичных. Когда требуется еще большая точность, применяются все менее обобщенные признаки, вплоть до первичных [58, 252].
При построении сложной картины мира ребенок начинает с грубых пространственных оценок объектов и только потом овладевает способностью выделять детали и осуществлять их анализ. На этом пути он движется от динамических и потому по необходимости обобщенных критериев к статистическим и потому сколь угодно детальным. Отсюда и целостность всех правосторонних представлений.
В процессе формирования правосторонних описаний зрительного объекта выделяются такие признаки его формы, которые характеризуют его одномоментно, выявляют его структурные свойства и пространственные взаимоотношения всех его частей. Признаки такого типа в отличие от логических левополушарных, вычисляемых рекурсивно, мы называем представлениями формы.
Среди целостных представлений формы рассматриваются скелет, регулярность, сложность, сходство. Формирование каждого из них включает пространственные операции (например, аффинные преобразования), которые существенно отличаются от логических и арифметических операций, таких, как суммирование и сравнение с порогом. Для получения скелетного представления (скелета) требуется произвести пространственное преобразование объекта — сжатие (рис. 20), для выявления регулярности — параллельный перенос, вращение, поворот относительно некоторой оси.

Разновидность регулярности — симметрия — классифицируется на зеркальную и поворотную (осевую и центральную) в зависимости от того, производится ли вращение плоскости изображения при ее выявлении. Симметричные изображения различаются по числу осей при зеркальной симметрии, по углу поворота — при центральной. Несимметричные фигуры также могут различаться по степени локальной регулярности.
Сложность рассматривается как правополушарное представление, поскольку ее вычисление включает в себя пространственные и динамические преобразования: выявление регулярности, учет расстояния повторяемого участка от начала осмотра контура и величин углов (кривизны огибающей), от которых зависит длительность зрительного анализа контура фигуры. Понимаемое как представление сходство обнаруживается при совпадении частей у объектов при их наложении друг на друга, т. е. при пространственных операциях, а мера сходства вычисляется как отношение величины совпадающих частей к общему числу деталей.
Операции соотнесения, необходимые для выявления перечисленных представлений, частично осуществляются во внешнем поле в реальном времени и пространстве, но могут выступать как мысленные вращения и наложения.
Превращение фигуры в собственную схему, скелет нацелена на упрощение сложного изображения (рис. 20). При формировании скелета объект непрерывно утоньшается и сглаживается вплоть до сохранения только элементов, составляющих его «каркас». Скелетное представление эффективно использовалось при решении многих задач, например при распознавании видов хромосомных болезней [274]. Нами скелет был использован для утоньшения изображения рукописных букв и папиллярных линий в качестве предварительной обработки их толстых изображений.
Скелет — целостное обобщение и упрощенное представление объекта. При его построении происходит загрубление, сглаживание локальных особенностей конфигурации. Информативность скелета определяется тем, что он сохраняет ряд таких значимых свойств исходного изображения, как связность, ориентация главной оси, симметрия.
В некотором смысле скелет — это правостороннее суждение. Он в явном виде присутствует в рисунках детей, когда они изображают у всадника обе ноги и тень, просвечивающие сквозь одежду. Важно отметить, что такое схематическое изображение облегчает переход к трехмерному представлению за счет подчеркивания связей и пространственных отношений. Поэтому по скелету можно восстановить пространственную конфигурацию частей объекта с точностью до класса, так как здесь не сохранены локальные свойства.
Для выделения скелета каждая точка объекта представляется как центр наибольшего круга, который целиком содержится в этом объеме, для точек контура радиусы таких кругов равны нулю. Скелетом объекта называется геометрическое место центров максимальных кругов, т. е. таких, которые не содержатся в других кругах. Эти центры вместе с радиусами соответствующих максимальных кругов определяют медиальную ось объекта. В случае фигур на квадратной сетке или цифровых картин при построении скелета вместо окружности используются квадраты [274].
Если оценить сложность фигуры и сложность ее скелета, то обнаруживается прямая корреляционная связь между оценками. Это дает возможность предполагать, что при узнавании фигур человек может использовать в качестве информативного замещения объектов их скелеты.
Продуктивность представления фигуры с помощью скелета становится более очевидной при описании трехмерных сцен или при опознании движущихся объектов. При движении объекта форма его изображения на сетчатке может настолько измениться, что возникает вопрос, является ли измененное изображение одной из трансформаций того же объекта, или это другой объект? Связность скелета и другие его свойства при движении исходного объекта в трехмерном пространстве меняются в меньшей степени, чем другие признаки изображения. Можно сказать, что помехоустойчивость скелета очень высока. Распознавание предшествующего и последующего положений исходного объекта (представленных скелетами) при его движении сводится к установлению изоморфизма графов.
В некотором смысле можно говорить о сложности, симметрии и скелете как о структурных представлениях объекта. Расположив эти три вида представлений в такой ряд, мы будем иметь либо более регулярное, либо более упрощенное представление.
Интересно, что еще 20 лет назад, проводя свои экспериментальные исследования восприятия тестовых фигур у детей 4-5 лет, мы заметили, что получив инструкцию разложить карточки с фигурами на две группы — хорошие и плохие, дети в первую из этих групп отобрали фигуры, симметричные с осью симметрии, а в другую — несимметричные и симметричные с центром симметрии. Уже тогда у нас возникло предположение, что восприятие различных видов симметрии требует от человека разных условий: труднее осуществить преобразование объекта для выявления у него центральной симметрии, чем зеркальной.
Это предположение [252] проверялось нами в дальнейших исследованиях восприятия фигур взрослыми здоровыми испытуемыми. При инструкции ранжировать фигуры по сложности обнаружилось, что субъективная сложность у фигур с центральной симметрией больше, чем с зеркальной. Это входило в противоречие с аналитическими оценками сложности формы, основанными на том, что чем больше степень регулярности, тем проще фигура. Субъективные оценки находились в обратном соотношении: фигуры с центром симметрии и обладавшие более высокой степенью регулярности, по сравнению с зеркально симметричными фигурами, оказались для человека более сложными, чем с осевой симметрией.
Для объяснения полученных результатов мы обратились к экспериментам Шепарда [278] по опознанию повернутых объектов. Он показал, что время, необходимое для принятия решения о том, что две картинки изображают повороты одного и того же объекта, линейно зависело от угла поворота между изображениями и мало зависело от направления этого поворота. Независимо от этого, установлено, что ошибки ротации наблюдаются при поражении правого полушария. Так, при функциональном отключении этого полушария по инструкции нарисовать или сложить фигуру, повернутую относительно оригинала на 180 или 90°, больные не справлялись с заданием. Очевидно, что с операцией мысленного поворота фигуры теснее связано правое полушарие.
Мы допустили, что существует некий механизм, организующий или кодирующий сложные фигуры в более простые. Этот процесс занимает время, поэтому обследование фигур с центральной симметрией требует дополнительных операций поворота фигур по отношению к восприятию зеркальной симметрии, что и делает их более сложными для человека. То, что первый вид симметрии усваивается ребенком позднее, также говорит о его большей субъективной сложности.
Все указанные обстоятельства нашли свое отражение в предложенном нами способе аналитического описания сложности фигуры, побудив учесть и то, что осмотр углов разной кривизны требует разных временных и операционных затрат, что хорошо согласуется и с рядом исследований. Очевидно, чем больше деталей содержит фигура, тем она сложнее и тем больше вероятность того, что выделенные элементы могут забываться или трансформироваться в памяти за интервал времени от ее восприятия до опознания и, следовательно, тем менее вероятно правильное ее распознавание. Если части фигуры идентичны друг другу, как в случае симметрии, можно выделить группы идентичных элементов в процессе восприятия и вероятность правильного опознания увеличивается. Эксперименты показали, что это справедливо только для фигур, содержащих больше элементов, чем можно запомнить за один раз, и недействительно для более простых фигур, где группировка по указанному принципу бессмысленна.
Отчетливо проявилась и другая особенность восприятия у взрослых: фигуры несимметричные, но по некоторым критериям близкие к симметричным субъективно воспринимаются как симметричные. Возможно, что их проще запомнить как правильные с коррекцией, чем как совсем нерегулярные. Так возникла задача определения и учета порога, при котором фигура уже воспринимается человеком как нерегулярная. В связи с этим в алгоритм вычисления сложности внесена поправка, учитывающая нагрузку на кратковременную память человека при восприятии формы.
Мы пришли к заключению, что для получения достаточно точной оценки сложности нельзя не учитывать характера операций человека с фигурой, поскольку ее объективные свойства соотносятся со способом, каким человек ее обследует и запоминает. Исходя из этого, мы положили в основу оценки сложности изображения метод А. Н. Колмогорова [95] и корректировали его с учетом экспериментальных данных.
Решение любых задач, с которыми непрерывно сталкивается человек, невозможно без предварительного накопления опыта, организации полученных знаний в системы, позволяющие эффективно использовать информацию при решении.
Знания о мире организуются в двух моделях мира по-разному. Если для правой характерны целостные системы, то для левой — классификационные. Целостным портретам справа, построенным при накоплении опыта тренировок, соответствуют деревья классификации слева. Портретам, сформированным при обозрении классов однотипных объектов с различных позиций, соответствуют классификации по признакам разных уровней.
Портреты и деревья представляют априорные сведения о классе объектов, которые в соответствии с нашей гипотезой используются человеком при распознавании. Учет специфики такой априорной информации дает нам возможность строить процедуры анализа, адекватные не только распознаваемым объектам, но и решаемым задачам, т. е. позволяющие оптимально вычленить из объектов значимые для распознавания области. Важно отметить, что при обучении формируются не только структуры хранения информации, но и другие вспомогательные структуры, которые управляют последовательностью право- и левополушарных обращений к отдельным зонам хранилищ в процессе распознавания. Среди разнообразия задач мы выбрали такие, что позволяют проиллюстрировать процесс накопления знаний, организацию их в специфические для правого и левого полушарий структуры, которые в дальнейшем можно использовать для узнавания. Как именно они включаются в процесс, мы проиллюстрируем при описании конкретных алгоритмов.
Оценивание сложности объекта, фигуры относится к наиболее распространенным операциям, осуществляемым человеком в качестве предварительной подготовки к разнообразным видам деятельности. Какой критерий использует человек для такой оценки, точно не известно. Выдвигались разные предположения, но их экспериментальная проверка не дала хорошего совпадения с разбиением, осуществляемым человеком. Кроме плохой корреляции все предложенные критерии недостаточно формализованы, что затрудняет их применение в технике и искусственном интеллекте.
Многие годы мы работаем над формализацией оценки сложности и распространением ее на все более широкие классы объектов. Раскроем содержание критерия «сложность» и покажем, что он адекватен оценке сложности зрительных фигур, осуществляемой и легко вычисляемой человеком. Мы предполагаем, что сложность может служить основанием классификации, а построенное по этому основанию дерево — использоваться в дальнейшем для распознавания объектов, например, накапливая сведения о форме листьев и плодов, человек постепенно приходит к заключению, что первые сложнее вторых. Он может использовать эти знания для различения при неполной информации, когда в ночной мгле цвет и объемные характеристики не воспринимаются, а виден только силуэт. Аналогично, увидев вычурный контур легкового автомобиля, человек заключает, что это машина старой марки, поскольку обводы современной машины более сглажены, обтекаемы.
Сопоставляя фигуры, ранжированные испытуемыми по сложности с использованием произвольного критерия, мы обнаружили интересный факт. Фигуры, оценивавшиеся ими как наиболее сложные, имели и наиболее «длинные» первичные коды. Эксперименты подкрепили нашу гипотезу о такой корреляции. Поскольку первичные коды позволяют однозначно восстанавливать фигуру и тем быстрее, чем короче ее первичный код, то наметилась аналогия с колмогоровским определением сложности некоторого сообщения информацией, необходимой для его восстановления [95]. А. Н. Колмогоров предложил измерять сложность двоичного слова наименьшей длиной программы, позволяющей однозначно описать это слово. Эту идею мы использовали для построения оценки сложности изображения (названной алгоритмической) по минимальной длине описания его формы в виде программы [58, 252, 253]. Необходимость модификации колмогоровской оценки определялась тем, что математическая теория, основанная на предложенном им универсальном оптимальном алгоритме, имеет сугубо асимптотический характер и не может быть применена к оценке сложности интересных с практической точки зрения изображений — фигур, деревьев и др.
Доводы в пользу применения алгоритмической оценки можно объединить в две группы. Первая включает в себя аргументы типа: если объект (фигура, слово и т. п.) содержит повторяющиеся части, то его описание может быть сокращено (уменьшается длина кода), так как при его кодировании достаточно воспроизвести повторяющуюся часть один раз и отметить сам факт повторения. Когда повторяемые куски присутствуют в объекте не целиком, а по частям и задается само расположение этих частей, можно рассматривать иерархию повторений.
Вторая группа доводов связана с возможностью определить сложность одного объекта через сложность другого, близкого к первому (близость здесь понимается в том смысле, что первый объект можно перевести во второй с помощью небольшого числа локальных операций). Приведенные соображения естественны и используются человеком при запоминании и узнавании фигур. В экспериментах обнаружилась достаточно сильная корреляция объективного критерия сложности, разработанного нами, с оценкой ее человеком. Одновременно выявились и некоторые отличия, связанные с особенностями зрительного восприятия человека. Алгоритмическая оценка сложности фигур как модификация относительной колмогоровской сложности учитывает экспериментальные данные о трудности восприятия человеком различных типов симметрии и регулярности.
Во многих экспериментальных исследованиях в качестве тестового материала используются фигуры более или менее произвольного вида. Однако процедуры построения фигур и вычисления характеристик, как правило, неоправданно сложны, отсутствуют также сведения о свойствах генеральной совокупности фигур. Стремясь к унификации результатов и автоматизации их обработки, мы создали специальный класс тестовых фигур, который свободен от упомянутых недостатков [57, 58, 253]. Достоинство этого класса фигур в их несмысловом характере, что позволяет исключить влияние предыстории человека, меняющей личную значимость объектов и дает возможиость рассматривать этот класс как аппроксимирующий для других, более общих. С помощью таких фигур мы провели многочисленные эксперименты по распознаванию, классификации, ранжированию, присваиванию наименования, в которых участвовали здоровые и больные испытуемые, взрослые и дети.
Каждая фигура основного (базового) класса — замкнутый многоугольник без самопересечений контура, его вершины расположены в узлах квадратной решетки, стороны имеют длину 1 или √2 (длина стороны или диагонали элементарного квадрата решетки), смежные стороны образуют углы 45, 90 и 135°. На рис. 19 приведены примеры базовых фигур. Простота построения этих фигур и вычисления признаков их формы, огромное разнообразие (для больших рангов) и вытекающая отсюда возможность целенаправленного создания тестовых наборов, автоматизация этих процедур с помощью компьютеров — все это делает предложенный класс удобным для экспериментов.
Расширенным назван класс замкнутых многоугольников без самопересечений контура с вершинами в узлах квадратной решетки, длина стороны может быть кратной 1 или √2. Фигуры в нем тоже несмысловые, но с их помощью можно аппроксимировать смысловые фигуры (рис. 21).

Форму зрительного объекта можно описывать в виде слова (кода), где каждая буква характеризует отдельный участок контура по локальному признаку. Для определения меры сложности фигуры ее код описывается программой, содержащей команды двух типов. Они выбраны потому, что лежат в основе алгоритма, управляющего движениями глаз человека при анализе фигуры. Первый тип — команда B(i, k) — построить угол с номером i k раз, второй — команда P(i, j, l, k) — повторить уже построенный фрагмент кода (аi, аi+1, ..., аj) с началом на i-м месте и концом на j-м месте k раз, начиная с l-го места.
За значение (алгоритмической) сложности изображения принимается минимальная длина его описания в виде программы в системе указанных команд, т. е. минимальная сумма длин записи команд программы. Команда повторить позволяет сокращать длину описания за счет повторяющихся блоков — регулярности: чем выше порядок симметрии, тем короче описание.
Психофизиологические исследования показали, что чем больше кривизна контура на данном участке фигуры, тем больше времени затрачивает человек на его анализ, тем сложнее этот участок для него. При построении адекватной его действиям оценки сложности мы учли это обстоятельство в нумерации углов:
Длина записи команды построить вычисляется по формуле
| B(i, k) | = 4 + [ log2 | 2i-7 | ] + [ log2 k ],
где квадратные скобки означают целую часть логарифма.
Длина записи команды повторить вычисляется по формуле
| P(i, j, l,k) | = 3 + [ log2 ( | i-j |+1 ) ] + [ log2 | l-i | ] + [ log2 k ] + [ log2 ε ],
В этой формуле учтены число повторений фрагмента, его удаленность от повторно воспринимаемого участка фигуры и длина этого участка. Все перечисленные моменты важны для человеческого восприятия в связи с ограниченностью объема его кратковременной памяти. Кроме того, результаты психологических исследований показали, что осевая (зеркальная) симметрия при прочих равных условиях проще для опознавания, чем центральная.
Наконец, особым типом регулярности формы является так называемая симметрия двойственности. В отличие от фигур с зеркальной симметрией, многоугольники с симметрией двойственности имеют попарно равные углы при отсутствии равенства соответственных заключающих их сторон. Фигуры с симметрией двойственности сложнее для восприятия, чем фигуры с зеркальной симметрией, имеющей такие же угловые коды. Все это учтено с помощью величины
2 при i < j (центральная, или поворотная симметрия)
ε = { 8 при l — i = 2, ai+1 ≠ π/2, 3π/2, i ≥ j (симметрия двойственности,)
1 в остальных случаях(зеркальная симметрия).
Понятие алгоритмической сложности легко обобщается на другие классы фигур, например, на произвольные неветвящиеся ломаные с ограниченной длиной. В последнем случае простая кривая аппроксимируется ломаной, которая кодируется в системе двух описанных команд. (В отличие от замкнутых фигур здесь циклические перестановки не рассматриваются, так как это ведет к получению других ломаных, минимизация кода осуществляется только за счет операций повторения.) Под сложностью односвязной замкнутой фигуры с криволинейным контуром понимается сложность аппроксимирующей ее фигуры с определенной степенью точности, где аппроксимирующая фигура принадлежит основному классу.
Многочисленные исследования [58, 252, 253] показали, что алгоритмическая оценка адекватна субъективной оценке сложности, использованной людьми при решении задачи упорядочения фигур по этому критерию. В эксперименте испытуемым предъявлялись фигуры в наборе из 10-25 штук. Участника просили разложить фигуры в ряд по сложности, при этом понятие сложности для испытуемых не раскрывалось. Всего в экспериментах приняли участие около 2 тыс. человек. Материал для ранжирования содержал 28 разных наборов, состоявших из фигур основного и расширенного классов, а также ломаные линии. Для каждого набора было получено не менее 20 рядов по субъективной сложности, по ним вычислялось среднее место каждой фигуры. Полученный ряд сравнивался с упорядочением этих фигур по «объективной» сложности — алгоритмической оценке и вычислялся коэффициент корреляции рангов Спирмена. Превышение коэффициентом (0,73-0,81) критических значений (0,49) для всех наборов фигур свидетельствует об адекватности разработанной оценки представлениям людей о сложности формы.
Убедившись в эффективности оценки для односвязных фигур, мы расширили ее на многосвязные объекты — композиции фигур: объединения двух и более базовых односвязных фигур с двухсвязной границей без самопересечения (так называемые «фигуры с дыркой»), n-связные фигуры (n ≥ 2), составленные из конгруэнтных фигур, а также односвязные фигуры с односвязным контуром (без дырок) с любым числом самопересечений. Оказалось, что принцип оценки может быть сохранен, однако необходимы поправки, учитывающие виды и характер композиции: число фигур в композиции, их расположение относительно друг друга, мера их сходства, наличие в композиции симметричных фигур и симметрии самой композиции.
Поправка ∆ учитывает число фигур (n) в композиции:
n — 1 при n > 2,
∆ = { 0 при n ≤ 2
Поправка α учитывает взаимное положение фигур в композиции:
— 6, если одна фигура находится внутри другой фигуры,
α = { 6, если вне фигуры.
Поправка ν=6 вводится для композиции, обладающей в целом центральной симметрией, для остальных композиций она равна нулю.
Поправка μ, отражает наличие в композиции фигур, обладающих зеркальной симметрией:
4 при n = 2, ψ = 90°,
5 при n = 2, ψ = 45°, μ = { —6 при n = 2, ψ = 45°,
—6 + n — np при n > 2,
0, если в композиции нет двух фигур с зеркальной симметрией,
где ψ — угол между осями симметрии двух зеркально симметричных фигур; np — число зеркально симметричных фигур с параллельными осями (ψ=0).
Поправка η=6 вводится при наличии двух похожих фигур, — тех, что совпадают при наложении их контуров (включая поворот в плоскости) по крайней мере в половине углов каждой из фигур, при этом площадь области пересечения фигур должна быть не меньше половины площади каждой фигуры. Если эти условия не соблюдаются, то поправка равна нулю.
В то время как при определении сложности базовой фигуры ее контур описывается кодом — такой последовательностью команд построить и повторить, которая дает минимальную длину записи кода, вычисление оценки сложности композиции начинается с построения кода композиции, где учитываются виды и уровни симметрии составляющих композицию отдельных базовых фигур и симметрия самой композиции.
Сложность композиции определяется как минимальная длина записи ее кода с учетом перечисленных поправок. Ниже приведены примеры вычисления сложности разных композиций, показанных на рис. 22 (углу 0° приписан нулевой номер i=0).

Пример 1. Композиция типа «фигура в фигуре» (рис. 22, а). Код внешней фигуры: B(5, 1) В (0, 1) B(2, 1) B(0, 1) P(4, 2, 5, 1) B(0, 1) P(8, 6, 9, 1) P(10, 2, 12, 1). Код внутренней фигуры: B(2, 1) B(1, 1) B(3, 1) P(23, 22, 24, 1) B(4, 1) B(0, 1) B(1, 1), B(5, 1).
Длина записи каждой команды вычислялась по формулам, указанным выше, при определении величины сложности C суммировались эти длины и поправка α. C=55.
Пример 2. Композиция в целом и базовые фигуры обладают зеркальной симметрией (рис. 22,б). Код композиции: B(2, 1) B(3, 1) B(1, 1) B(5, 1) P(3, 3, 5, 1) P(6, 1, 7, 3). Поправки α, ∆, μ. C=36. Здесь первые пять команд — код одной фигуры, последняя команда формирует композицию.
Пример 3. Композиция обладает центральной (поворотной) симметрией, а фигуры в ней — зеркальной симметрией (рис. 22, в). Код композиции: B(2, 1) B(3, 1) B(1, 1) B(5, 1) P(3, 2, 15, 1) P(6, 1, 7, 3). Поправки α, ∆, μ, ν. C=42.
Пример 4. Композиция обладает центральной симметрией, а фигуры несимметричные (рис. 22, г). Код композиции: B(2, 1) B(0, 1) B(1, 1) B(5, 1) B(1, 1) B(3, 2) P(7, 1, 8, 3). Поправки α, ∆, ν. C=48,5.
Пример 5. Композиция состоит из фигур с совпадающими участками на контурах (рис. 22, д). Формирование кода начинается с фигуры, имеющей меньший по длине контур (меньшее число углов), здесь — с верхней фигуры: B(0, 1) B(2, 1) B(0, 1) B(2, 2) B(5, 1) P(6, 1, 7, 1). Код нижней фигуры — P(12, 1, 13, 1), он состоит только из команды повторить, т. е. незаштрихованная часть фигуры не кодируется. Поправки α и η. C=40.
Для проверки адекватности предложенной оценки сложности композиций субъективной оценке их сложности были проведены экспериментальные исследования ранжирования. В экспериментах участвовали 156 человек. Материалом экспериментов служили шесть наборов по 25 композиций. (В качестве рассмотренных выше примеров вычисления сложности (рис. 22) взяты композиции из этих тестовых наборов.) Анализ результатов экспериментов показал, что значение коэффициента корреляции рангов Спирмена для каждого набора варьировало в пределах 0,67-0,80, существенно превышая критическое значение 0,49, что свидетельствует о высокой прямой корреляционной связи между теоретической сложностью фигур и оценкой их человеком.
Разновидностью описанной выше оценки служит сложность фигур еще одного класса. Здесь фигура — замкнутая ломаная линия с восемью вершинами и максимальным числом точек пересечений — девять. Такие фигуры назывались «траекториями». Испытуемому предъявлялся набор траекторий, каждая на карточке 10X10 см. Примеры траекторий приведены на рис. 23. Набор состоял из 10-11 фигур, исследовались семь наборов, всего 63 различные траектории. В экспериментах участвовало 123 человека.

Сложность траектории вычислялась как минимальная длина программы, содержащей только одну команду — построить угол α — В (α), где α — величина угла. При описании траектории с помощью этой команды кодировались внутренние углы в вершинах ломаной, а в точках пересечений — наименьший из углов. Длина записи команды определялась по следующему соотношению:
| α | 1-2° | 3-14° | 15° | 30° | 45° | 60° | 75° | 90° | 105° | 120° | 150° | 155-179° | 180° | 360° |
| B(α) | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0,5 | 12 |
Сложность левой траектории на рис. 23 равна 43, правой — 101. Сопоставление рядов траекторий, упорядоченных по сложности испытуемыми и в соответствии с теоретической оценкой, показало, что между ними существует высокая корреляция. Коэффициент корреляции рангов Спирмена (0,80-0,88) превышал критические значения 0,56 и мало варьировал от набора к набору.
Изучая класс тестовых фигур, описанных в книге Боно [234], мы использовали вариацию описанного подхода для оценки их сложности. Суть ее в построении некоторой дополнительной фигуры (форма которой отражает взаимное расположение фигур в композиции) — оболочки, внешней по отношению к композиции. Область внутри оболочки, не принадлежащая фигурам композиции, называлась заполнителем. Суммарная сложность оболочки и заполнителя дает информацию о сложности каждой из фигур этой композиции и о сложности их взаимоотношения.

На рис. 24 показаны примеры различных композиций Боно. Видно, что контуры оболочки и заполнителя могут совпадать во многих местах композиции, где образуются новые углы, что создает «лишнюю» сложность. Для ее устранения введен коэффициент 2/3, понижающий сложность композиции (СC), вычисляемую как сумму сложностей оболочки (СЕ) и заполнителя (СI):
CC = 2/3( CE + CI )
Код оболочки первой композиции на рис 24: B(2, 1) B(0, 4) B(5, 1) B(0, 1) B(2, 2) B(0, 4) P(1, 13, 14, 1). СE=27,5. Код заполнителя: B(2, 1) B(0, 1) B(2, 2) B(5, 1) B(0, 2) P(1, 7, 8, 1). СI = 25. СC = 35. Сложности остальных композиций рис. 24 равны соответственно: 48,5; 52,5 и 64.
Экспериментально проверена и эта оценка. Испытуемые (50 человек) ранжировали фигуры Боно, материалом служили два набора из 14 фигур каждый; коэффициенты корреляции рангов Спирмена составляли 0,83 и 0,87. Корреляция между субъективной сложностью композиций Боно и теоретической ее оценкой, вычисленной с помощью основного подхода (без заполнителя), также существенно превышала критическое значение, хотя и была несколько ниже, чем при подходе с оболочками — заполнителями. Однако недостаток второго метода состоит в том, что для фигур с большим разнообразием углов оболочки и соответственно заполнителя неоднозначны: оболочка и заполнитель создают углы, не свойственные исходной композиции.
Итак, чтобы вычленить значимую информацию для формализации сложности как критерия классификации, изучались действия разных людей с различными объектами. Существо оценки состоит в моделировании и измерении трудоемкости зрительного анализа для человека. Чем больше общая длина осмотра при движении в одном направлении и чем больше локальных возвратов приходится делать на этом пути, тем выше трудность анализа объекта, его сложность. В качестве самой существенной информации для оценки сложности выявлены степень регулярности и количество возвратов, на них основан формальный критерий.
Важно отметить, что разработанная оценка сложности отдельной фигуры может вычисляться независимо от сложности других фигур, входящих в предъявляемую совокупность. Конечно, это не исключает того, что, будучи предъявленной в другой совокупности, данная фигура несколько изменяет свою субъективную сложность, но, как показали наши эксперименты, эти изменения обычно незначительны. В то же время все другие методы, используемые для измерения сложности фигуры психологами, позволяют оценить ее сложность только в заданной совокупности, что резко затрудняет использование таких результатов в других условиях без специальных исследований.
Предложенные до сих пор оценки субъективной и объективной сложности формы (и наши в том числе) не отражают одного важного феномена. Экспериментально обнаружено, что субъективная сложность фигуры не растет до бесконечности: при достижении сложностью некоторого значения фигура скачком вновь кажется простой. Возможно, в этот момент человек перестает воспринимать контур объекта и начинает оперировать с его огибающей, тогда субъективная сложность огибающей вновь может расти до следующего сброса. Функция сложности предстает как ступенчатая.
Поскольку количественный критерий сложности сформулирован, можно строить систему классификации объектов по сложности и переходить к распознаванию по сложности. Описанный критерий сложности по своей сути правосторонний.
Снижение активности правого полушария ведет к облегчению восприятия ахроматических цветов: это полушарие тесно связано с цветоразличением. Возникла идея проверить экспериментально, изменится ли стратегия действий испытуемых при классификации фигур по сложности и сходству, когда люди имеют дело не с черными, а с цветными фигурами. Если цвет-признак скорее правосторонний, то форма может восприниматься и обрабатываться и в правосторонней и в левосторонней метрике. Пример первого случая — представление фигуры скелетом, второго — кодом вторичных признаков. Контрольными материалами служили результаты наших исследований с черно-белыми фигурами при решении этих задач [57, 58, 253].
Испытуемым предлагалось разложить карточки с изображениями фигур на две группы. В одном случае в качестве критерия разделения выступало сходство, в другом — сложность. Материалом служили наборы из 25 карточек размером 7Х7 см, на каждой карточке изображена тестовая фигура — силуэтная, определенного цвета на белом фоне, занимавшая приблизительно половину площади карточки. В исследованиях участвовало 846 человек обоего пола. Использовалось четыре набора (A, B, C, D) при классификации изображений по сходству и два набора (A, C) при классификации их по сложности. Фигуры во всех наборах — многоугольники основного класса, в наборах A и B — 12-угольники, в C и D — 10-угольники.
Испытуемому предъявлялись одновременно все фигуры набора одноцветных фигур (всего использовалось пять цветов: желтый, коричневый, зеленый, синий, красный) либо разноцветных (всех пяти цветов, по пять фигур каждого цвета). Предлагалась инструкция: «Разложите фигуры на две группы по сходству». Понятие сходства не определялось. Аналогичное задание испытуемый получал перед классификацией изображений по сложности, менялась только формулировка критерия. С каждым набором по одному критерию работало не менее 20 человек.
Результаты эксперимента оформлялись в виде матрицы наблюдений, каждая ее строка — разбиение, выполненное одним человеком, столбец — номер фигуры в наборе. Автоматически выделялось ядро — совокупность фигур, которые попали в одну группу не менее, чем у 80% испытуемых, работавших с данным набором. Ядро (его состав и размер — число фигур) служило характеристикой единообразия стратегий испытуемых [59]. Так, если в ядро вошли все фигуры из набора, это означает, что все испытуемые одинаково разложили их на две группы — стратегии у них совпадают на 100%.
| Набор фигур | В наборе фигуры одного цвета | В наборе фигуры | ||||||
| желтый | красный | зеленый | коричневый | синий | среднее | черного цвета | пяти цветов | |
| Классификация по сложности | ||||||||
| C | 16 | 18 | 12 | 14 | 18 | 15 | 15 | - |
| A | 17 | 14 | 14 | 13 | 14 | 14 | 22 | - |
| Классификация по сходству | ||||||||
| C | 15 | 20 | 21 | 20 | 20 | 19 | 15 | 18 |
| D | 17 | 8 | 13 | 16 | 9 | 12 | - | - |
| A | 12 | 7 | 5 | 5 | 9 | 7 | 6 | 7 |
| B | 9 | 6 | 7 | 3 | 5 | 6 | - | - |
Размеры ядер, полученных при классификации одноцветных фигур по сложности, приведены в табл. 1. Из нее следует, что средний размер ядра набора C составил 15 (61% от общего числа фигур в наборе) и он тот же, что и для черных фигур, т. е. разнообразие цветов не отразилось на стратегии классификации фигур этого набора. Если сопоставить ядра наборов фигур различного цвета по составу, то оказывается, что десять фигур тождественны у ядер всех пяти цветов (рис. 25).

Анализ формы фигур, составляющих ядра, показывает, что ведущим признаком для разделения изображений по сложности для наборов C и A служила симметрия. Средний размер ядра одноцветных фигур набора A составил 14, а что касается состава ядра, то девять фигур тождественны у всех цветов. Можно отметить некоторую тенденцию к уменьшению единообразия работы испытуемых при повышении ранга фигур (числа углов), т. е. при увеличении субъективной трудности задачи, что подтверждает ранее полученный нами результат. Вместе с тем при классификации цветных и черных фигур набора A проявилось существенное различие в размере ядра: при работе с черными фигурами единообразие стратегий составило 88%, а с цветными — в среднем 56%. Вероятно, в последнем случае цвет несколько осложнил действия испытуемых.
Обсуждая результаты классификации фигур по сходству, следует отметить, что набор D отличался от набора C большим разнообразием формы: фигуры того же ранга, но подобраны так, чтобы уменьшить априорное объективное сходство между фигурами в наборе. Набор B отличался от набора A большим сходством формы: фигуры того же ранга, но подобраны так, чтобы увеличить названное сходство.
Из табл. 1 видно, что средний размер ядра в случае одноцветных фигур набора С фактически тот же, что и для разноцветных фигур, но превысил этот показатель для черных фигур Можно допустить, что цвет облегчил действия испытуемых при классификации фигур этого набора по сходству. При анализе состава фигур ядер одноцветных наборов С выяснилось, что 15 одинаковых фигур входили в ядра всех пяти цветов, а сравнение состава общего одноцветного ядра с ядром разноцветного набора выявило у них 14 одинаковых фигур. Таким образом, цвет не оказывал существенного влияния на классификацию по сходству.
Средний размер ядра одноцветных фигур набора В меньше, чем средний размер его для набора А. Таким образом, при увеличении априорного сходства между фигурами задача для испытуемых стала более трудной, и эта тенденция не зависела от цвета фигур.
Рассматривая состав ядер набора А, мы установили, что не существует ни одной фигуры, которая входила бы в ядро наборов всех цветов. Следовательно, здесь цвет значительно повлиял на действия испытуемых. Сравнивая ядра наборов А и В, видим, что наибольшие размеры у желтого цвета, наименьшие — у коричневого. Таким образом, при классификации фигур этих наборов по сходству цвет влиял на стратегию испытуемых: проще всего им было работать с желтым цветом и труднее всего — с коричневым.
Эксперименты по классификации позволили сделать следующий вывод. Симметрия выступала ведущим признаком при разделении фигур по сложности и не служила таковым при разделении по сходству. Влияние формы как разделяющего, критерия оказалось более сильным, чем влияние цвета и проявилось в большей мере при классификации по сходству, чем по сложности.
Участнику других экспериментов — по распознаванию — предъявляли эталонную фигуру, затем ее убирали, после чего ему предъявляли тестовую таблицу (серия) из 25 фигур (5x5), среди которых находился и эталон. Необходимо было опознать эталонную фигуру в таблице, при этом фиксировался правильный ответ или ошибка. Фигуры в тестовой таблице А были те же, что и в наборе А, аналогично — в таблице С. Эталонами служили три фигуры каждого набора. Из шести эталонов три были симметричными, их номера 2, 3, 5. Каждый эталон предъявлялся не менее чем 20 испытуемым, не участвовавшим в экспериментах по классификации. Серии были либо одноцветные (использовались те же пять цветов, что и при классификации), либо из фигур пяти цветов (разноцветные — по пять фигур каждого цвета).
Субъективная трудность распознавания эталона вычислялась как отношение (в процентах) количества ошибок к общему числу предъявлений эталона.
Результаты для фигур одного цвета приведены в табл. 2. Упорядочивая эталоны .по возрастанию числа ошибок, допущенных при распознавании в обоих сериях, можно заключить, что субъективно более простыми эталонами оказались симметричные фигуры. Если упорядочить цвета по возрастанию среднего числа ошибок распознавания одного эталона, то для обеих серий полученные последовательности оказались сходными.
| Цвет эталона | Таблица A | Таблица C | ||||||
| номер эталона | среднее | номер эталона | среднее | |||||
| 1 | 3 | 5 | 2 | 4 | 6 | |||
| синий | 80 | 5 | 50 | 45 | 0 | 65 | 45 | 37 |
| коричневый | 25 | 5 | 10 | 13 | 0 | 40 | 40 | 27 |
| зеленый | 70 | 15 | 55 | 47 | 15 | 50 | 30 | 32 |
| красный | 45 | 25 | 40 | 37 | 15 | 60 | 70 | 48 |
| желтый | 65 | 25 | 65 | 52 | 0 | 70 | 75 | 48 |
| среднее | 57 | 15 | 44 | 6 | 57 | 52 | ||
| Цвет эталона | Таблица A | Таблица C | ||||||
| номер эталона | среднее | номер эталона | среднее | |||||
| 1 | 3 | 5 | 2 | 4 | 6 | |||
| синий | 10 | 5 | 40 | 18 | 0 | 40 | 60 | 33 |
| коричневый | 40 | 5 | 40 | 28 | 0 | 50 | 50 | 33 |
| зеленый | 48 | 15 | 35 | 33 | 10 | 60 | 30 | 33 |
| красный | 70 | 20 | 50 | 47 | 0 | 75 | 75 | 50 |
| желтый | 80 | 20 | 50 | 50 | 0 | 65 | 75 | 47 |
| среднее | 50 | 13 | 43 | 2 | 58 | 58 | ||
Вырисовывается общая тенденция: синий цвет — наиболее простой для распознавания, красный и желтый — наиболее трудные, независимо от формы.
Результаты распознавания эталонов разных цветов в сериях A и C, содержавших фигуры всех цветов, также приведены в табл. 2. Если выстроить разные по форме эталоны обеих серий в порядке возрастания среднего числа ошибок распознавания, то получим ряд, где субъективно более простыми опять оказываются симметричные фигуры. При этом наиболее легким для распознавания оказался коричневый цвет, а наиболее трудным — желтый.
Рассматривая решение испытуемыми трех видов зрительных задач — классификацию объектов по сложности и сходству, распознавание эталона, можно отметить, что влияние цвета усиливается при движении от первой задачи к третьей, а влияние формы при этом ослабляется. Поэтому вопрос о том, какую информацию кодировать формой, а какую — цветом, должен решаться в зависимости от вида задачи, которую решает человек.
Таким образом, исследование показало, что если люди классифицируют фигуры различных цветов по сложности, то их действия не зависят от цвета — классификация идет по регулярности (симметрии) так же, как классификация черно-белых объектов. Если классифицируются фигуры различных цветов по сходству, то действия людей с объектами разных цветов различны — классификация идет по многим различным признакам. Цвет определяет стратегию действий испытуемых при классификации по сходству, а при классификации по другому критерию — сложности — люди безразличны к цвету.
В этом разделе обратимся к еще одной операции, свойственной правосторонним преобразованиям в памяти, и покажем на примере музыкальных ритмов, как формируется такая структура знаний как обобщенный портрет.
В отличие от других важных элементов музыкального языка ритм принадлежит еще и языкам поэзии и танца и в этом плане может служить типовым примером организации таких временных структур, как метр, темп.
Как известно, значение ритма для выразительности музыки очень велико. Ритм сам по себе может характеризовать некоторые жанры музыки — марш, вальс и т. п. В плане данной книги существенно, что, будучи синонимом понятия регулярности, ритм присущ каждому произведению. Регулярность музыкального произведения проявляется как бы на трех уровнях. Первый — наиболее высокий — это строение музыкального произведения, так называемая его форма, второй — повторение (репризы и вариации) отдельных музыкальных предложений внутри частей, третий — регуляция на уровне тактов. Отметим, что из-за последовательного характера ритма, его линейности (слуховой образ) невозможно провести полную аналогию между ним и уровнями симметрии одномоментно воспринимаемых зрительных фигур.
В соответствии с общепринятыми определениями, размер — это нотное (символьное) изображение метра посредством обозначения его доли определенной длительностью, а всей метрической группы долей — дробью, где числитель указывает на количество долей размера, а знаменатель — на длительность, которая принята за основную (единичную) долю. Простыми называются метры и размеры, имеющие две или три доли при одном акценте. Наиболее распространенные из них — 2/4, 3/4, 3/8.

Далее описана попытка предоставить ритмическую структуру нескольких музыкальных произведений в виде единой зрительной картины. Для этого предварительно перекодировали нотную запись — сочетания длительности звучания нот в такте n-дольного музыкального размера (n=4, 8, 16...) описаны как отдельные группы и названы ритмическими ячейками. Например, в восьмидольном размере, где за наименьшую длительность принята восьмая доля такта, она обозначена как 1, а двух-, трех- и четырехкратные длительности — соответственно как 2, 3, 4. Тогда возможные ритмические ячейки в размере 2/4 составляют следующую совокупность (множество) (рис. 26,а):
(4), (3 1), (2 2), (1 3), (1 2 1), (2 1 1), (1 1 2), (1 1 1 1).
Такая кодировка позволяет представить ритмический узор как последовательность ритмических ячеек.
Переход между двумя ячейками аналитически описывается преобразованием Di. Преобразование порядка i действует над такими двумя первыми компонентами ячейки, которые в сумме дают i, таким образом, что из первой вычитается единица и прибавляется ко второй, при этом могут вставляться нули. Согласно этому правилу, переход между ячейками (5 1) и (4 2) соответствует преобразованию D 6, а между (4 2) и (3 1 2) — преобразованию D4 (здесь между 4 и 2 вставляется нуль).
Переходы между ритмическими ячейками зрительно представляются в виде ориентированного графа с ячейками в его вершинах. На рис. 27 показан граф для размера 3/4 (6/8). 32 ячейки этого графа включают длительности от одной восьмой (1) до шести восьмых (6). Очевидно, что стороны шестиугольника на графе соответствуют преобразованиям D6, пятиугольника — D5, квадрата — D4, треугольника — DЗ, «двуугольника» — D2. Переход между ячейками, не соседствующими на графе, описывается, суперпозицией преобразований Di. (Подобный подход к описанию ритма предложен Е. А. Трофимовой.)
Описанное кодирование позволяет представить ритм практически любого произведения, написанного в n-дольном размере (n = 2, 4, 8, 16,..), в форме пути на графе. Этот путь — как бы зрительный одномоментный портрет ритмики произведения, пространственный отпечаток его временной структуры. В качестве примера ячейки ритмического портрета «Менуэта» Моцарта (ноты его показаны на рис. 26, б) выделены с помощью кружков на рис. 27.

Граф переходов между ритмическими ячейками всех восьмидольных размеров обладает сложной структурой, в которой прослеживается многоуровневая регулярность (рис. 28). В основе структуры — восьмиугольник (для простоты он показан отдельно в центре), к его вершинам «прикреплены» подграфы, основы которых, в свою очередь, составляют n-угольники с меньшим числом углов (n=7, 6, 5, ... , 2). Подграфы соответствуют простым музыкальным размерам 7/8, 6/8(3/4), 5/8, 4/8(2/4), 3/8, 2/8(1/4). Сложные музыкальные размеры можно представить как результат слияния ритмических элементов одного размера, а смешанные — ритмических элементов разных простых размеров. Более распространены среди сложных размеров следующие: 4/4 = 2(2/4), 6/4 = 2(3/4), 6/8 = 2(3/8), 9/8 = 3(3/8), 12/8 = 4(3/8). Среди смешанных размеров распространены такие: 5/4 = 3/4 + 2/4, 5/8 = 2/8 + 3/8.

Для зрительного представления ритмики сложных и смешанных размеров введены дополнительные преобразования и полученные графы можно классифицировать по виду и степени симметрии. Так, граф для размера 12/8 обладает двумя осями и центром симметрии с углом поворота 90°, у графов для размеров 6/8 и 2/4 одна ось симметрии и центр симметрии с углом поворота 180°, у 9/8 — центр симметрии с углом поворота 120°, а у 5/8 и 5/4 нет симметрии. Таким образом, появилась возможность сопоставить часто встречающимся сложным и смешанным ритмическим музыкальным размерам аналогичные уровни симметрии зрительных фигур.
Построив граф для ритмики отдельного произведения, можно сформировать обобщенный портрет совокупности музыкальных пьес. Такой портрет был синтезирован по принципу наложения, как при построении обобщенного портрета человека — представителя конкретной национальности. Для этого ритмические портреты ряда пьес, написанных в одинаковом размере, накладывались друг на друга и каждой ячейке на суммарной графе приписывался вес, равный частоте ее использования в анализируемых произведениях. Обобщенный портрет включал ячейки с весом, не меньшим, чем 10% от суммарной частоты всех использованных ячеек в рассмотренных пьесах.
Таким методом были синтезированы обобщенные портреты для нескольких групп музыкальных пьес — всего были проанализированы 53 пьесы, написанные в размере 3/4. В первую группу входили двадцать классических вальсов Глинки, Шопена, Штрауса, Чайковского, Грига. Во вторую — шесть романсов в стиле вальса, принадлежавших перу Беккера, Шатрова, Джойса, Кюсе. В третью группу были включены семь романсов Грига, в четвертую — четыре джазовых вальса: Брубека, Превэна, Питерсона, Саркина. Пятую составляли русские народные песни: «Веселая беседушка», «Раненый казак», «Я вечор в лужках гуляла», «По долу гуляет», «Девушка крапивушку жала». Шестая группа включала шесть украинских народных песен: «Выйди, выйди, ой, Иваньку», «Павук сiрий», «Пусти мене, милый», «Горе же мене, горе», «Ой, рано, рано», «Чи чули, ви, люде». И, наконец, седьмая группа была сформирована из пяти популярных песен 40-х годов нашего века: «Синий платочек», «Моя любимая», «Случайный вальс», «Священная война», «Дороги».
Анализ ритмики рассмотренных произведений показал [233], что в них использованы не все возможные 32 ячейки в размере 3/4, а лишь 26 из них. Обобщенный портрет одной группы состоял из 3-5 ячеек. Для классических вальсов его составляли четыре ячейки: (6), (4 2), (2 2 2), (1 1 1 1 1 1); романсов в стиле вальса — также четыре: (6), (1 1 3 1), (3 2 1), (2 1 1 1 1); у джазовых вальсов оказался наибольший по составу обобщенный портрет — пять ячеек: (6), (4 2), (2 2 2), (1 1 1 1 2), (1 1 1 1 1 1). В портрете популярных песен и украинских народных песен всего по три ячейки: (6), (4 2), (2 2 2) и (2 1 1 1 1), (1 1 4), (1 1 2 2); наконец, портрет рассмотренных русских народных песен содержал четыре ячейки: (4 2), (2 2 2), (1 1 2 2), (4 1 1).
Итак, совокупность обобщенных ритмических портретов содержала только 12 ячеек, из них три — (6), (4 2), (2 2 2) — входят в наибольшее число проанализированных портретов. В известном смысле можно сказать, что часть графа, включающая эти три ячейки, составляет как бы общее ядро обобщенных (портретов, а другие ячейки отражают особенности ритмики отдельных классов музыкальных произведений, например (3 2 1), (1 1 3 1) и (1 1 3 1) специфичны только для обобщенного ритмического портрета проанализированных романсов Грига.
Глядя на обобщенный портрет, легко понять, на чем базируется узнаваемость данного класса музыкальных произведений. Человек не осознает критерии различения, поскольку, как мы думаем, он опирается при распознавании на обобщенный портрет, сохраняемый в правосторонней эпизодической, автобиографической памяти, используемой подсознательно. При этом он опирается на те же процессы, благодаря которым может отличить незнакомый ему язык, например немецкий от французского.
Полученные обобщенные портреты ритмики включают меньшую часть всех возможных вершин графа соответствующего музыкального размера. Отсюда явно обозримым становится поле приложения усилий для будущего творчества композиторов и систем искусственного интеллекта, способных к синтезу музыки. Кроме того, анализ обобщенных портретов произведений, созданных в разное время, дает информацию о тенденциях в изменении узоров ритмики в историческом плане, что позволяет на основе экстраполяции предсказывать направление будущих течений в ритмической структуре музыкальных пьес или синтезировать музыку с заданными свойствами.
Всякому распознаванию предшествует классификация, в процессе которой формулируются описания классов. В памяти левосторонней модели описание класса сопоставляется с набором признаков, принадлежащих элементам класса, и эти признаки организованы в виде дерева. Представление совокупности однотипных объектов в памяти правой модели отливается в общий портрет — пространственную структуру, отражающую не только общность контуров, но и взаимное положение их частей.
Здесь даны краткие описания идей, положенных в основу использованных нами алгоритмов распознавания изображений разного типа: лиц, рукописных букв, дефокусированных фигур, папиллярных узоров. Во всех алгоритмах объект представляется в виде каркаса. Форма каркаса выступает как обобщенный портрет класса (правая модель), а количественные характеристики каркаса — как признаки из левой модели. Эффективность процесса распознавания — отнесения объекта к классу — определяется обоими способами описания и своевременностью обращения к механизмам правой и левой моделей мира [11, 20 21, 22, 232, 250].
Если исходить из того, что у каждого взрослого человека сформировано представление о лице в виде обобщенного портрета, то анализ его свидетельствует об определенном взаимном расположении отдельных черт: нос находится между глазами, рот — ниже носа, волосы — выше глаз, а подбородок — ниже рта. Эти общие сведения использованы как знания, полученные предварительно и позволяющие строить гипотезы с целью распознавания портрета, а также сделать его обработку экономной. Кроме того, учитывается информация о различной значимости черт идентификации: в классификационном дереве ведущие места занимают глаза и рот. Изображения на рис. 29 служат наглядной иллюстрацией для этого тезиса, основанного на массе экспериментальных данных.

Стратегия распознавания связана с построением «несущей конструкции» лица — треугольника, образованного центрами наиболее информативных областей — глаз и рта, и анализ изображения нацелен на их выделение. Характерологический треугольник с вершинами в центрах областей глаз и рта служит представлением данного конкретного лица и используется для его распознавания, отражая пространственное соотношение между чертами лица, наименее меняющееся в зависимости от возраста и эмоции, в этом смысле он выступает как целостное правостороннее описание.
Распознаванию подвергались реальные фотопортреты, которые предварительно обрабатывались. С этой целью была создана группа алгоритмов, которые можно использовать в разных комбинациях при обработке изображений, представленных в виде дискретных матриц яркостей. В каждом из алгоритмов применены приемы, позволяющие исключить полный перебор анализируемых точек изображения и минимизировать их число. Наряду с моментами, специфическими для каждого алгоритма, они содержат ряд общих идей.
Исходным материалом при реализации алгоритмов служили фотопортреты анфас размером 60Х90 мм (рис. 30, а), переведенные в форму дискретной матрицы яркостей 220Х170 элементов специальным устройством путем сканирования обычного негатива. Градации яркостей — элементы матрицы — варьировали в диапазоне 0-255. Лицо занимало на портрете не менее половины площади. Исходная матрица обрабатывалась с помощью алгоритма выделения контуров, основанного на пороговой процедуре. Пороговое значение перепада яркости определялось автоматически и зависело от яркости данного первичного изображения. В результате работы этого алгоритма исходное многотоновое изображение преобразовывалось во вторичное, каждая точка которого либо принадлежит контуру — черная, либо нет — белая (рис. 30, в).

На основе предынформации о взаимном расположении черт лица на изображении строилась вспомогательная конструкция из сечений — трех вертикальных и трех горизонтальных — с таким расчетом, что они определенно пересекали область глаз и рта. Сечения проводились по трем столбцам и трем строкам матрицы яркостей на расстоянии одна треть, половина, две трети длины соответствующей стороны рамки изображения. Параметры решетки, образованной сечениями, определены на основе знаний о конструкции любого лица. На области глаз и рта приходится наибольшее число контурных линий, а также неоднородных по яркости пятен. Поэтому в алгоритмах выделения контуров и однородных областей для определения порогов достаточно было использовать информацию о распределении яркостей элементов только на сечениях и не было необходимости сканировать всю матрицу, как это делается в традиционных алгоритмах обработки «серых» изображений.
Порог вычислялся двойным усреднением модулей разности значений яркости в соседних точках сечения. Результатом первого усреднения было число, определявшее среднюю контрастность изображения, при втором усреднении учитывались только перепады больше средней контрастности.
Для отслеживания контура на изображении выделялись «стартовые» точки на сечениях — один из пары соседних элементов матрицы, где перепад больше порога. От каждой из них производился поиск контура в направлении, перпендикулярном данному сечению в обе стороны от него. Поиск определялся следующим рекуррентным алгоритмом. В окрестности текущей опорной точки (т. е. уже выделенной точки контура) проверялись пять вариантов — пять пар смежных точек. Если перепад яркости для какой-либо пары был больше или равен значению порога, то более «темная» точка пары становилась новой опорной и поиск продолжался, если продолжения не находилось, то считалось, что данная линия контура обрывается. Когда встречалась точка, через которую уже прошел контур, поиск продолжения данной линии прекращался — так избегалось зацикливание [11, 22, 253].
Полученное вторичное изображение содержало участки с различной концентрацией контурных (черных) точек. Наибольшее сгущение черных точек приходилось, очевидно, на области глаз и рта. Цель последующей обработки вторичного изображения — отделение этих областей от других областей с высокой концентрацией контуров.
Следующий алгоритм — выделение больших однородных областей — преобразовывал исходное многотоновое изображение во вторичное с меньшим числом градаций — 3-4 (рис. 30,б). Значения самих градаций определялись автоматически и зависели от яркости данного исходного изображения.
Так, при трехградационном варианте пороги определялись следующим образом. Анализировались элементы на шести упомянутых выше сечениях, на каждом выделялись участки с непрерывными перепадами яркостей у соседних элементов, равными единице и превосходящими ее. М — число выделенных участков, они упорядочивались по среднему значению яркости элемента в каждом таком участке Вi(i=1, 2, ..., М): В1<В2< ... <ВМ. Вычислялся минимальный перепад между соседними членами полученной последовательности: Rmax1 = max | Вi-Вi+1 |. Если Rmax1 < ( BM-B1 ) / 4, то процедура повторялась для перепадов, равным двум и более единиц яркости, и так далее, пока не выполнялось условие Rmaxj ≥ ( BM-B1 ) / 4. Тогда определялись величины двух порогов для данного сечения D1 = ∑Bj / i и D2 = ∑ Bj / M — i, затем — средние значения для всех сечений — это и были искомые два порога. Теперь яркости, превосходившие больший из этих порогов, считались черным тоном, меньшие меньшего порога — белым, в интервале между порогами — серым.
Для выделения однородных областей трех тонов первичное изображение сканировалось при помощи окна 7Х7. Если каждый элемент в окне был того же тона, что и его центральный элемент, то окно маркировалось этим тоном, в противном случае значения исходной яркости у элементов окна не менялись. Таким образом, полученное вторичное изображение содержало области белого, серого и черного тонов, а также участки с исходной яркостью, которые не вошли в однородные области, из-за выраженной неоднородности элементов.
Цель последующей обработки вторичного изображения — отделение областей глаз и рта. На вторичное изображение (контурное или трехтоновое) вновь накладывалась сетка из шести сечений, которые просматривались с целью выделения участков с наибольшим сгущением контурных точек либо участки с наиболее выраженной неравномерностью.
Анализ относительного положения и границ участков сгущений с учетом априорных знаний о взаимном расположении черт лица давал границы трех прямоугольных областей, включавших глаза и рот, последняя область фактически могла содержать конец носа и рот, если они очень близко расположены у данного человека. Каждая из трех полученных подматриц исследовалась более подробно теми же алгоритмами предобработки с целью выделения центра области. Сформированный характерологический треугольник использовался при идентификации. Он сравнивался с вариантами допустимой деформации лица, хранящегося в памяти распознающей системы, накопленными при обучении, позволяя опознавать данного человека. Если при обучении в память записывается по одному треугольнику для каждого человека, а тренировочная последовательность — набор взаимного положения и формы треугольников для каждого человека в различных эмоциональных состояниях (удовлетворение, радость, восторг, покой, грусть, гнев, горе) (рис. 31), то можно распознавать не только человека, но и его эмоциональное состояние. Алгоритм распознавания эмоциональных состояний реализован для фотопортретов шести мужчин и шести женщин в нескольких эмоциональных состояниях и показал высокую эффективность.

Таким образом, в процессе решения задачи распознавания лиц попеременно использовались левосторонние признаки — при исследовании каждого сечения и правосторонние представления — сетка сечений, характерологический треугольник. Каждый из алгоритмов можно соотнести с циклами спиралевидного процесса передачи информации между правой и левой моделями мира.
Рукописные буквы невозможно распознать, не используя знания, накопленные при обучении и хранящиеся в памяти виде классификационных систем признаков. В этом отношении примененные подходы к распознаванию лиц и букв сходны между собой. Отличие в том, что если при узнавании лиц было достаточно одного дерева в структуре памяти, то для букв этого оказалось мало — использовались семь деревьев. «Лес» деревьев породил специальную структуру, управляющую переходом от одного дерева к другому по мере развития процесса распознавания буквы. Эта структура тоже состояла из двух деревьев, и, в конечном счете, девять деревьев составляли систему памяти.
Алгоритм реализован для распознавания рукописных букв русского алфавита. Рассмотрены 102 класса топологически различных написаний тонких букв (рис. 32). Исследовано 1709 изображений, все они могут быть получены аффинными преобразованиями представителей этих классов. Изображения букв были представлены в виде бинарных матриц 25x20 элементов, нули образовали фон, а единицы — собственно букву [21, 60, 180, 253].

Использованы два метода описания изображения буквы: первый — построение касательных и анализ граничных точек на них, второй — построение профилей и анализ их характера. Распознаванием руководило дерево признаков, сопоставлявших изображению буквы набор признаков.
Левой (правой) касательной считался самый левый (правый) ненулевой столбец матрицы, соответственно верхней (нижней) касательной — самая верхняя (нижняя) ненулевая строка. Касательные играли роль каркаса буквы. Одновременно с построением касательных производилось выделение на них граничных точек — таких точек буквы, что лежали на касательной: очевидно, что граничная точка могла принадлежать не более чем двум касательным одновременно.
В качестве признака, характеризовавшего граничную точку, использовался порядок узла — число линий, входивших в данную граничную точку и выходивших из нее. Признак порядок узла можно сопоставить с локальным признаком кривизна участка контура. Поскольку изображения дискретны, между двумя линиями возможны углы 45, 90 и 135°. Граничная точка считалась узлом второго порядка, если она образована только двумя линиями с углом между ними 45 или 90°, а граничные точки, не являвшиеся узлами, считались касаниями — узлами нулевого порядка — им могут соответствовать углы 135 или 180°. Для определения порядка граничные точки анализировались с помощью 5- или 9-окрестностей, которые выступали как усеченные варианты традиционных 8- и 16-окрестностей. Такое уменьшение поля анализа позволяли сведения о том, какая именно касательная анализируется — в соответствующей части окрестности граничной точки заведомо нет точки изображения. В качестве левостороннего обобщенного — позиционного — признака, характеризующего совокупность граничных точек буквы на определенной касательной, использовалась функция следование за... по ходу сканирования касательной.
Изучение взаимного расположения граничных точек на каждой касательной для разных классов букв позволило сформулировать правила опознания в соответствии с типом касательной и построить четыре разделяющих дерева признаков граничных точек — для каждой из четырех касательных. При формировании дерева использовались сведения о реально существующих цепочках граничных точек на данной касательной — так дерево признаков упрощалось на основе априорного знания о типе анализируемых изображений.
Изучение типов граничных точек на каждой касательной и сведения о конечном числе их комбинаций позволили прогнозировать тип некоторых граничных точек, не рассматривая их окрестности. Это существенно ускорило процесс распознавания: так, использование информации по левой касательной ограничило число анализируемых граничных точек до двух-трех, причем для третьей, а в ряде случаев и для второй точек достаточно было лишь выявления факта ее существования. Если граничных точек четыре, то тип четвертой граничной точки всегда предсказывался без ее анализа. Соответствующие правила сформулированы для граничных точек на остальных касательных, и на их основе построены разделяющие деревья.
Буква анализировалась и при построении так называемого профиля. Левым (правым, верхним) профилем называлось описание части изображения буквы, «видимого» со стороны одноименной касательной. Форма профиля характеризовалась с помощью графика функции расстояния от соответствующей касательной до изображения (рис. 33). Поскольку график строился с некоторым шагом, который определялся по числу и типу граничных точек и их взаимному расположению, профиль формировался после построения и анализа соответствующей касательной.

Профиль описывался с помощью локальных признаков — участков выпуклости и вогнутости с положительным и отрицательным значением первой производной на графике функции расстояния, а также прямолинейных участков на этом графике. Шаг построения и анализа профиля мог быть разным на различных участках одного и того же профиля. Нижний профиль никогда не формировался. Соответственно трем профилям построены три разделяющих дерева по одному правилу. Выбор вида функции расстояния дал возможность анализировать не весь профиль, а лишь ту его часть, которая соответствует отрезку касательной, где нет граничных точек.
Распознавание букв включает в себя три этапа. На низшем определяются значения локальных признаков — порядок узла и форма профиля. На следующем анализируются разделяющие деревья признаков граничных точек и профилей, где содержится информация о взаимоотношении локальных признаков. Если первый уровень дает только описание изображения буквы, то второй позволяет вырабатывать гипотезы о классе, к которому может быть оно отнесено, и управлять их проверкой.
Третий уровень представлен деревом признаков для классов и деревом взаимодействия процессов двух более низких уровней. Третий уровень указывает на последовательность обращений к процессам низших уровней, т. е. предметом описания здесь служит не изображение буквы с признаками, характеризующими ее форму, а стратегия ее обследования при распознавании. Аналогами локальных признаков низших уровней (порядок узла, форма профиля) на верхнем служат процедуры обращения к анализу граничных точек, профилей. На верхнем уровне используется тот же позиционный признак следования за, т. е. процедура обращения к деревьям второго уровня с упорядочением их следования. Дерево взаимодействия между уровнями формируется в процессе распознавания и составляет процедурное знание, в то время как деревья признаков граничных точек и профилей — декларативное.
Анализ более чем 1700 написаний букв показал, что большинство их кончается линией-связкой, поэтому почти у всех букв русского алфавита наиболее часто встречающаяся граничная точка на правой касательной — это узел первого порядка. Отсюда следует, что признаки граничных точек на правой касательной не могут служить эффективным разделяющим признаком. Аналогично для нижней касательной: написания большинства букв либо касаются ее, либо имеют на ней узлы первого и второго порядков. В результате — все написания букв разделяются с помощью комбинаций узлов разного порядка и касаний на одной касательной на 17 групп для левой и верхней касательных. Но при этом суммарное число вхождений различных написаний одной и той же буквы в группу, выделенную по левой касательной, меньше, чем по верхней, т. е. левая касательная информативнее, чем верхняя. Таким образом, для русского языка граничные точки на левой касательной позволяют произвести наиболее эффективное разделение написаний букв на группы с различными локальными признаками. Экспериментальные исследования тоже показали, что при узнавании людьми наиболее информативными оказались верхняя и левая часть русских букв.
Для рукописных букв ряда других алфавитов наиболее информативной при распознавании оказалась также левая касательная для алфавитов английского, грузинского и хинди, в то время как для армянского, арабского, персидского и урду важнее верхняя касательная, что, вероятно, связано со способом письма.
С учетом сказанного понятно, что работа алгоритма начиналась с построения левой касательной как наиболее информативной. Ее анализ приводит в вершину первого уровня дерева принятия решений. Если она концевая — распознавание заканчивается. Это справедливо для восьми изображений, что составляет 0,47% от общего числа исследованных написаний. Если вершина первого уровня промежуточная, то строится следующая касательная (какая она — определяет дерево взаимодействия уровней) или профиль.
Количество осматриваемых точек изображения при движении по ветвям дерева межуровневого взаимодействия при всех комбинациях касательных и профилей оценивается как
Ccp = ∑ piCi,
где i — число узлов на этом дереве, pi — удельный вес числа изображений, распознанных в данном узле дерева принятия решений; Ci — среднее число просмотренных течек изображения буквы. При реализации алгоритма указанная оценка получила вид
Ccp ≤ 2,41m + 1,45n + 0,54mn + 18,85,
где m — высота выпуклой оболочки, натянутой на знак, n — ее ширина. При этом подавляющее большинство написаний — 83% — требуют при распознавании просмотра меньшего, чем среднее число точек матрицы. Самое большое число элементов матрицы просматривается при разделении пар букв ш-щ и и-ц, где нужно выделить узел четвертого порядка в правой части изображения, для них число рассмотренных точек в 4-5 раз превышало среднее. Подобных пар написаний всего 13, что составляет меньше 2% от общего числа распознаваемых знаков. Очевидно, что сокращение перебора точек изображения при распознавании влечет за собой сокращение времени работы алгоритма. Алгоритм не чувствителен к метрическим преобразованиям, не изменяющим топологические особенности изображения, допускается наклон изображения вправо и влево от вертикали на угол не более чем 45°.
Эффективность алгоритма мы оцениваем степенью сокращения перебора точек изображения букв при распознавании. Такой подход к оценке удобен, так как не зависит от распознающего устройства. Оценка складывается из частных оценок числа элементов, анализируемых при исследовании всех типов граничных точек [180]. Реализация алгоритма показала, что для распознавания русских рукописных букв в среднем требуется проанализировать только треть точек на их изображении. В программном продукте учтена однотипность обработки наборов признаков — база данных для классов изображений построена так, что позволяет обрабатывать с помощью одной и той же процедуры информацию, полученную при анализе различных касательных и профилей. Это позволило сократить объем и число процедур обработки и сделало распознающую систему легко перенастраиваемой на другие изображения — другой алфавит, цифры, графики и т. п.
Две предыдущие задачи распознавания — лиц и букв — содержали ограниченное число объектов: в первом случае один, во втором — тридцать один. Описываемая ниже задача содержит неограниченное число классов. Такая ее специфика определила особенность накопления и организации априорной информации об объектах. Распознаванию подлежали изображения дефокусированных фигур. Каждый класс включал исходную фигуру (не подвергавшуюся дефокусировке) и ряд ее трансформаций как результат разной степени дефокусирования. Для накопления априорной информации использовалось представление фигуры в виде каркаса. Его форма была выбрана в соответствии со сведениями об особенности деформирующего влияния дефокусировки: центральная часть фигуры (более удаленная от ее контура) разрушается меньше, чем периферия фигуры, прилежащая к контуру.
Если в задаче распознавания рукописных букв понадобилась структура, содержащая деревья классификации тридцать одного класса букв по признакам формы (граничным точкам и профилям), то в задаче о деформированных фигурах при обучении формировались пять деревьев классификации по признакам формы, что соответствовало пяти уровням дефокусировки 50 классов фигур. В процессе распознавания специальное управляющее дерево определяло адрес обращения к одному из деревьев классификации, а затем уже выбирало путь на этом дереве.
У проблемы распознавания разрушенных и зашумленных объектов своя специфика — либо невозможно выделить контур, либо эта операция весьма трудоемка. С другой стороны, человек успешно справляется с решением задачи идентификации объектов и в условиях плохой видимости. Можно предположить, что эффективность и помехоустойчивость при обработке подобных изображений обеспечивается главным образом за счет восприятия целостности, связности механизмами правого полушария.
Традиционный способ распознавания разрушенной фигуры основан на восстановлении формы и выделении ее контура. Этот подход хорошо разработан, широко применяется, но оказывается мало эффективным, если объект разрушен сильно или предъявляется на фоне больших шумов. В таком случае исходный контур выделяется либо не целиком, либо при этом появляются многочисленные дополнительные контуры (объект зашумлен), либо вообще нельзя говорить об исходном контуре после сильного размытия или дефокусирования объекта.
В реальных практических ситуациях размытые и зашумленные изображения встречаются часто. Такие условия создаются при необходимости узнавать предметы в непогоду (снег, дождь, туман), через преломляющую среду (толща воды, газа, пара) и т. д. Эффект размытия фигур может возникнуть и при уменьшении контраста фигуры с фоном, в частности, за счет цвета фигуры, мало контрастного по отношению к фону.
Пытаясь понять, как человек справляется с этой трудной задачей, мы пришли к заключению, что, работая с неповрежденными контурами, когда время решения не ограничено и требуется высокая точность, он может эффективно использовать методы обработки информации, присущие левому полушарию, а сталкиваясь с сильно разрушенными объектами, особенно в дефиците времени, он делает упор на структурные методы обработки информации, присущие правому полушарию. В последнем случае он прежде всего выдвигает гипотезу о возможной форме разрушенного объекта, базируясь на совокупности фрагментов объекта, которые еще можно разглядеть, и проверяет ее, пытаясь реконструировать объект на основе этих фрагментов. Используя подобную стратегию, мы применили алгоритм, который выделяет отдельные фрагменты изображения, подвергшиеся разрушению в наименьшей степени, и организует их в некоторую структуру, однозначно соотносимую с формой исходного (неразрушенного) объекта, что дает возможность произвести распознавание [20].
На первом этапе из изображения выделялись наименее разрушенные области — каркас. Это правосторонняя процедура. Затем включались левосторонние операции, классифицировавшие области на группы по критериям их формы. Новый цикл также состоял из правосторонних и левосторонних операций и так далее, вплоть до удовлетворительного распознавания. Когда объект распознан, т. е. отнесен к определенному классу, можно было реконструировать его исходную, неповрежденную форму.
Объектами распознавания служили 50 фигур того же основного класса, который использовался как тестовый материал при исследовании зрительного восприятия. Изображение, содержавшее фигуру, было представлено матрицей яркости 40Х40, где элементы с единичной яркостью принадлежали фону, а с яркостью в интервале 2-15 — фигуре (объекту). В случае неразмытой фигуры матрица двухградационная: у элементов фона яркость равна единице, у элементов объекта — 15. В общем случае — размытая фигура — матрица 15-градационная. На рис. 34 показан пример резкой (неповрежденной) фигуры и четыре варианта ее дефокусирования в порядке возрастания его степени.

Собственно распознаванию предшествовала обработка исходных изображений, нацеленная на формирование экономного и эффективного представления фигур. На первой стадии обработки осуществлялось загрубление градаций яркости исходного изображения: заданный интервал из 15 градаций разбивался на пять отрезков по три градации, яркость отрезков изображалась пятью символами ● (точка), Г, П, К, Ж в порядке возрастания значения яркости. Так производилось первое сжатие информации: вместо исходной матрицы двузначных чисел получена матрица символов. Далее на полученном изображении выделялась область, занимаемая фигурой. Для этого строилась оболочка — прямоугольник, сторонами которого служили крайние сверху и снизу строки и крайние справа и слева столбцы матрицы, содержавшие только элементы-точки. Дальнейшему исследованию подвергалась полученная подматрица, ограниченная оболочкой (область фигуры), в ней выделялись центральная строка (горизонтальная ось), центральный столбец (вертикальная ось), а также элементы, лежавшие на двух диагональных осях, составлявших угол 45° к центральной строке.
На следующей стадии анализу подвергалась полученная структура — каркас — совокупность элементов изображения на четырех осях при четырех градациях яркости — самая низкая градация (точка) не рассматривалась. В этой совокупности не более чем 168 элементов (4x40 + 8), второе слагаемое связано с обозначением номеров восьми полуосей. Таким образом произошло новое сжатие информации.
Далее каркас подлежал анализу с целью определения степени размытия фигуры, которую он представлял. Если все элементы каркаса были максимальной яркости из возможных четырех, то фигура резкая (неразмытая) — нулевая степень размытия. Когда на каркасе находились элементы всех четырех градаций яркости, фигура слабо размыта — степень размытия равнялась двум. Когда каркас состоял из элементов трех градаций яркости, кроме самой высокой, и при этом элементы наибольшей из этих трех градаций попадались на всех осях, а также число наиболее ярких элементов превышало по отдельности числа элементов каждой из двух меньших градаций, степень размытия фигуры равнялась четырем. Если на каркасе попадались элементы этих же трех градаций яркости, но при этом число наиболее ярких элементов меньше по отдельности числа элементов каждой из двух меньших градаций, то степень размытия равнялась шести. В случае, когда каркас состоял из элементов двух меньших градаций яркости и при этом число более ярких элементов было не ниже, чем менее ярких, степень размытия равнялась шести, а при обратном соотношении чисел более и менее ярких элементов степень размытия была максимальной — восемь. И, наконец, если каркас состоял только из наименее ярких элементов, то фигура также была размыта максимально — степень восемь.
Информация, подлежащая дальнейшему анализу, вновь сокращалась: на каркасе отсекались ветви, содержавшие наименее яркие элементы — оставшиеся элементы каркаса представляли наименее разрушенную часть фигуры.
Таким образом, анализ состава элементов каркаса позволял определить степень размытия представляемой им фигуры. Отнесение усеченного каркаса к одному из классов фигур производилось с помощью дерева соответственно степени размытия.
Дерево распознавания для каждой степени размытия содержало четыре яруса с одинаковым набором разделительных признаков. На рис. 35 приведено такое дерево для фигур при наиболее сильной дефокусировке. Из четырех признаков три — левосторонние обобщенные (вторичные): вытянутость А, эксцентриситет Е, изогнутость В, а симметрия S — правосторонний.

Вытянутость характеризовала относительную протяженность фигуры вдоль каждой из четырех осей каркаса. Проверялись два условия. Первое удовлетворяется, если отношение длин двух наибольших осей равно или превышает 1,5 (длина оси равна числу элементов изображения на ней). Второе условие удовлетворяется, если отношение длин двух наименьших осей меньше 1,5. Градации признака соответствовали тому, удовлетворяются или нет оба условия или только одно из них.
Эксцентриситет центра тяжести характеризовал соотношение частей фигуры, расположенных по разные стороны от некоторой оси каркаса. Для его определения выбирались наименьшая по длине ось каркаса и те, что отличались от нее не более, чем в 1,5 раза. Если выбранных осей несколько, то фиксировалась та, которая делилась центром каркаса по полуоси с меньшим отношением по длине. Рассматривались две совокупности по три полуоси по разные стороны от фиксированной оси. Градации признака соответствовали отношению суммарных длин указанных совокупностей.
Изогнутость вычислялась как число перепадов между длинами соседних полуосей каркаса, этот признак имеет наименьшее значение у фигуры типа правильного шестиугольника и наибольшее — у звезды.
Симметрия характеризовала регулярность фигуры. Она определялась следующим образом. Каркас, представленный как упорядоченная последовательность восьми полуосей, обозначался словом из восьми букв, где буквы кодировали длины полуосей. Тогда слово wxyzzyxw соответствует каркасу с одной осью зеркальной симметрии, слово wxxvvxxw — каркасу с двумя осями зеркальной симметрии, wxyzwxyz — поворотной симметрии, wxyzwxyu — почти поворотной симметрии и, наконец, sytxwxyz — несимметричному каркасу.
Использованный подход к описанию дефокусированных изображений проявил свою эффективность не только в высоком уровне правильного распознавания, но и в существенном сокращении перебора анализируемых точек на обрабатываемых изображениях при машинной реализации описанного алгоритма за счет использования лишь небольшой части входной информации при вынесении решения как при обучении, так и при самом распознавании. Так, с помощью левосторонних признаков и правостороннего представления — каркаса — были расклассифицированы и распознаны 250 фигур из 50 классов с общим результатом — 10% ошибок для всех пяти степеней размытия, при этом для четырех (исключая самую высокую) — 5%, для самой высокой — 23%.
По сравнению с ранее рассмотренными задачами распознавание папиллярных узоров (отпечатков пальцев) представляется самой сложной. Генетическая эволюция человека — прижизненная и историческая — отпечатывается в виде неравномерностей на поверхности кожи, составляющих папиллярный узор, где однозначно отображаются также изменения и нарушения в ходе эволюции. Этот узор можно рассматривать как результат интерференции многих процессов, которые существенно отличаются друг от друга временными и пространственными характеристиками.
Известно, что папиллярные линии — это гребешки кожи, образующие узор на подушечках пальцев, ладонях и ступнях ног человека. Они строго индивидуальны и остаются неизменными в течение всей жизни человека, на этом основана дактилоскопия. Пальцевые (папиллярные) узоры, согласно классификации криминалистов, предложенной в конце прошлого века, разделяются на типы: дуга, петля, завиток. При предварительной классификации отдельный предъявленный отпечаток должен быть отнесен к одному из этих принятых классов, а последующая идентификация требует информации об особенностях папиллярного узора конкретного человека.
Большинство существующих подходов к автоматическому описанию и классификации отпечатков пальцев основано на том, что признаки выделяются в процессе анализа папиллярных линий: при этом все линии считаются равнозначными, поэтому для вычисления признаков необходимо полное отслеживание всех линий по их протяженности. Лишь в отдельных работах поле папиллярного узора разбивается на зоны и поиск определенных характеристик узора производится в этих зонах. Это первые шаги на пути отказа от полного построчного сканирования всего отпечатка пальца или полного покомпонентного его просмотра.
Решая первую часть задачи — отнесение узора к одному из трех классов — мы использовали предварительную априорную информацию, накопленную криминалистами, а также наши представления о специфике формы папиллярных узоров, согласно которым отпечаток рассматривается как информационное поле, определенные зоны которого упорядочены, согласно введенной нами иерархии уровней их значимости. Это позволило сократить объем анализируемой информации — анализ папиллярного узора не предусматривает сканирования всего поля и выполняется скачкообразным переходом от одной значимой зоны к другой, при этом подтверждается или отвергается гипотеза, выдвинутая в результате анализа информации в предыдущей зоне.
Изображения отпечатков пальцев (называемые далее отпечатками) были представлены бинарными матрицами яркостей 256X256, единичные элементы матрицы соответствовали темным местам на реальном отпечатке, нулевые — светлым. Мы рассматривали идеальный отпечаток в том смысле, что он не содержал уровней серого тона и шума. Кроме того, он полный, т. е. получен полным «прокатыванием» подушечки верхней фаланги пальца. С другой стороны, отпечаток не идеален в том смысле, что папиллярные линии не обязательно тонкие.
На рис. 36, а приведены примеры реальных отпечатков, а на 36, б — топологические схемы трех типов. Одна из деталей узора — дельта — характеризуется слиянием трех потоков линий получила свое название, видимо, от сходства с этой буквой. У петлевого узора одна характерная дельта (справа или слева от центра — правая или левая петля), у завитка две дельты — справа и слева от центра, а у дуги дельт нет.

Для выявления характерных особенностей трех типов папиллярных узоров мы изучили более ста реальных отпечатков, выбранных в качестве представителей наибольшего различия внутри каждого из типов.
Стратегия обработки отпечатка для его классификации сводилась к выявлению на нем значимых областей, где три потока линий образуют дельту. Для этого изображение ограничивалось снизу прямой горизонтальной линией, которая проводилась посредине узкой белой области — горизонтальной полоски, отделяющей изображение подушечки верхней фаланги пальца от средней. Построенная линия составляла нижнюю сторону (базу) прямоугольной рамки, описываемой около отпечатка. Левая и правая стороны рамки — касательные к узору, перпендикулярные к базе, а верхняя касается узора сверху и параллельна базе. Внутри рамки проводились диагонали и другие линии, как показано на рис. 36, б. Таким образом, формировался некий каркас, представлявший взаимное положение зон на отпечатке, значимых для выявления дельт или их отсутствия.
Исследование реальных отпечатков показало, что с наибольшей вероятностью дельты расположены в зонах, прилегающих к нижним диагональным полуосям. Поиск дельт в этих зонах производится с помощью анализа следов линий в окне — подматрице изображения размером 40X40 элементов, диагональ окна составляет 60% длины диагональной полуоси каркаса.
Для поиска дельт на первом шаге использовались два окна, которые устанавливались слева и справа симметрично относительно вертикальной оси рамки так, что диагональ каждого окна находилась на соответствующей нижней диагональной полуоси каркаса и сдвинута от центра области внутри рамки к ее краю на одну пятую длины отрезка диагональной полуоси. Анализ направлений папиллярных линий в окнах относительно .диагональных полуосей каркаса позволяет выдвинуть гипотезу о принадлежности данного отпечатка к завиткам (в обоих окнах дельты или линии, «перпендикулярные» диагонали каркаса), к петлям (в одном окне дельта или линии, перпендикулярные диагонали, а в другом — линии, «параллельные» диагонали) или к дугам (линии в обоих окнах параллельны соответствующим диагоналям).
Признаком направления линий в окне служило соотношение числа следов — пересечений линиями в окне той его диагонали, что совпадает с соответствующей диагональю каркаса (она названа главной), и числа пересечений линиями окна другой его диагонали. Если первое из чисел больше второго, то дельта находится либо в окне, либо поблизости от него в данном квадранте отпечатка. Такой же вывод можно сделать, если первое число меньше второго и разность между ними не превышает четырех. В случае, когда первое число меньше второго на четыре или более единиц, выдвигается гипотеза об отсутствии дельты в окне и соответствующем квадранте отпечатка.
Подтверждение выдвинутой на первом шаге гипотезы осуществлялось на втором шаге. Здесь исследовались два других окна такого же размера, их центры смещены по соответствующим диагональным полуосям в направлении от центра каркаса к его периферии на 20 элементов по отношению к центрам соответствующих окон первого шага. Правило определения направления линий в окне второго шага то же самое. В том случае, когда на втором шаге не подтвердилась гипотеза, выдвинутая на первом шаге, анализируются диагонали одного или двух окон третьего шага. Исследование сотен реальных отпечатков показало, что, как правило, двух шагов (четырех окон) достаточно для завершения классификации, а третий шаг — наверняка последний.
Таким образом, для классификации отпечатка достаточно исследовать отдельные окна в нижней части изображения папиллярного узора, при этом не требуется анализа всех точек изображения внутри окна. Анализ значимых зон в верхней половине, над окнами первого шага позволяет произвести поиск «головки» узора, что, в свою очередь, дает возможность вычислить дополнительные признаки, характеризующие некоторые важные индивидуальные особенности данного отпечатка, например, число линий между центром и дельтой, наклон линий в головке и др. Но даже если все 1600 точек окна просматриваются при поиске центра головки узора, то это составляет только 2% от общего числа точек в исходном изображении папиллярного узора.
Автоматическая классификация позволяет существенно сократить поиск информации в картотеке, где хранятся отпечатки пальцев обеих рук большого числа людей. Существуют всего 66 комбинаций узоров трех классов на 10 пальцах. Известно, что петли встречаются в 65% всех папиллярных узоров пальцев рук, завитки — в 30, а дуги — в 5%. Тогда вероятность встречаемости различных комбинаций равна
p = ( 65i + 30j + 5k ) / 220,
где i — число петель, j — завитков, k — дуг среди отпечатков пальцев обеих рук, 220 — встречаемость отпечатков каждого типа во всех 66 комбинациях. Каждая из этих комбинаций, кроме тех, где все десять отпечатков принадлежат одному и тому же типу, подразделяются на равновероятностные варианты; их число В = С10ixC10-ii. Тогда вероятность каждого такого варианта — именно с ними имеют дело на практике — определяется как Р1 = Р/В. Вычисления приведенных величин показывают, что наибольшую вероятность имеют два варианта: все 110 узоров — петли (2,9%) и все 10 — завитки (1,4%). Все остальные комбинации встречаются не чаще, чем в 0,28% случаев каждый.
Так, если в картотеке хранятся отпечатки пальцев обеих рук 600 тысяч человек и для идентификации представлены отпечатки одного человека, при этом машинная процедура классификации установила, что на семи пальцах петли, на трех — завитки (вероятность такой комбинации 0,021%), то из картотеки отбираются только 1260 карточек, а эксперту будет предъявлено значительно меньшее их количество, поскольку проведенная классификация дала информацию о типе узора на каждом конкретном пальце.
Таким образом, автоматическая классификация предъявленных отпечатков на три класса позволила существенно ускорить последующую идентификацию, производимую экспертом.
* * * * * * *
В этой главе мы представили решение семи задач. Все они, продиктованные прикладными потребностями, доведены до компьютерной реализации. В каждой из них исследована самостоятельная научная проблема, новая либо по самой постановке (оценка взаимодействия цвета и формы в зрительных задачах, одномоментное зрительное представление системы музыкальных ритмов), либо по возможности решения (все описанные задачи — распознавания и количественной оценки сложности фигур).
Эти задачи имеют общий подход к решению. Так, при решении каждой из них используются не только обычные логические и алгоритмические способы решения (по нашей терминологии — левополушарные), но еще пока не включаемые в решение актуальных задач — аналоговые, целостные. В этом случае формируются такие правополушарные критерии, как каркасы, касательные, рамки. Важно отметить, что включаются эти признаки в решение задачи не последовательно (сначала одни, потом другие), а циклически, сменяя друг друга, направляемые исходной предварительной информацией и построенной на этой базе гипотезой. Для того чтобы организовать эффективное построение гипотезы, знания представляются в структурах графов и деревьев. При этом, как уже неоднократно упоминалось, в каждом полушарии своя память и поэтому правые и левые признаки опираются и на разный объем памяти, и на отличающиеся способы ее объединения. Тем самым и достигается содержательное продвижение на каждом шаге.
Во всех задачах в качестве цели выступало не просто получение решения как такового (при определенной точности), а получение решения экономичного, т. е. с минимальными затратами времени на анализ входной информации и ее хранение. Данный аспект решения обеспечивался во всех задачах за счет сокращения перебора элементов изображения на каждом этапе его анализа и обработки механизмами обоих типов.
Экономичность выполнения данных задач обязана общему бионическому и психологическому подходам к их решению, что указывает на возможный путь построения эффективных систем искусственного интеллекта. В частности, становится возможным, уменьшить размеры матрицы изображения по мере ее анализа и сократить число процедур обработки при той же точности решения. Это отличается от распространенной тенденции связывать решение новых зрительных задач с прогрессом технологии и оборудования (компьютеров) —увеличением размера матрицы изображения и параллельной его обработкой.
Динамика решения в концептуальном плане связана с анализом определенного поля памяти. С этой целью необходимо выявить в конкретной структуре памяти значимые части и элементы (отсечь ненужное) и тем самым первично сузить класс исследуемых на данном шаге гипотез. Нечто похожее выполняют эксперты, когда дают рекомендации по построению и информационному наполнению экспертных систем.
Три из описанных в этой главе задачи можно рассматривать как примеры искусственных систем, моделирующих некоторые моменты формирования структур знаний, четыре — как комплексно возникающие в распознающих и экспертных системах, моделирующие некоторые принципы и механизмы естественного интеллекта.